Bạn có bao giờ từng hỏi: "Con số lớn nhất là gì?", câu trả lời e rằng khó có thể có đáp án cụ thể. Tuy nhiên, bạn có tin con số 43.252.003.274.489.856.000 [Đọc là: 43 tỷ tỷ 252 triệu tỷ 3 nghìn tỷ 274 tỷ 489 triệu 856 nghìn] là số lượng cách sắp xếp trật tự cho một vật rất quen thuộc với đời sống chúng ta?
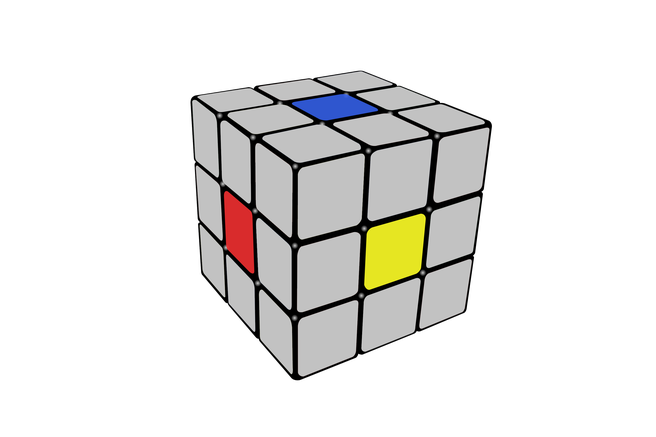
Câu trả lời đó là khối lập phương Rubik tiểu chuẩn 3×3×3.
Khối Rubik (còn gọi là Lập phương Rubik hay Rubik) là một trò chơi giải đố cơ học được Giáo sư kiến trúc, nhà điêu khắc gia người Hungary Ernő Rubik (sinh năm 1944) phát minh vào năm 1974. Khối Rubik hiện đại thường làm bằng nhựa, có 4 phiên bản chính là: 2×2×2 ("Khối bỏ túi"), 3×3×3 (Khối tiêu chuẩn), 4×4×4 ("Rubik báo thù") và 5×5×5 ("Rubik giáo sư").
Khối Rubik tiêu chuẩn sẽ có các mặt hiển thị một màu duy nhất, câu đố bắt đầu khi ta trộn các mặt lại với nhau, để mix ra một khối màu nhiều màu sắc. Việc của người chơi là sắp xếp lại chúng về hình dạng ban đầu (các màu không bị xáo trộn). Và con số 43.252.003.274.489.856.000 chính là số lượng cách sắp xếp trật tự của Rubik 3×3×3.
Câu hỏi đặt ra là: Tại sao một khối lập phương phiên bản 3×3×3 lại có thể cho ra số sắp xếp khổng lồ đến vậy? Để tính toán con số này, trước tiên chúng ta cần nhớ lại khái niệm hoán vị và định hướng.
1. HOÁN VỊ
Giả sử chúng ta có 3 quả bóng màu đỏ-xanh lá cây-xanh dương. Đề bài yêu cầu: Có bao nhiêu cách sắp xếp 3 quả bóng (3 màu khác nhau) cùng một hàng?

Chúng ta biết rằng các quả bóng có thể được sắp xếp theo nhiều cách khác nhau, nhưng chúng ta không biết có bao nhiêu hoán vị mà các quả bóng có. Để tìm số lượng hoán vị có thể, chúng ta có thể sắp xếp bóng một cách thủ công và trực quan nhất theo tất cả các cách có thể.

Vậy, tổng số hoán vị cho 3 quả bóng là 6. Đáp án này rất dễ tìm ra vì chúng ta chỉ có 3 quả bóng và dễ dàng sắp xếp chúng trực quan.
Nếu con số quả bóng tăng lên gấp 100 lần (tức là 300 quả bóng) thì có bao nhiêu hoán vị cho 300 quả bóng 3 màu đó? Sẽ mất một thời gian dài nếu chúng ta làm thủ công cách sắp xếp 300 quả bóng, vậy có cách nào khác để tính ra số hoán vị này?
Chúng ta cần sử dụng một phương pháp khác để giải quyết vấn đề, đó là sử dụng giai thừa. Trong toán học, giai thừa (ký hiệu là !) là kết quả của việc nhân một chuỗi các số tự nhiên giảm dần.
Ví dụ, cho n số tự nhiên dương, giai thừa của n bằng số hoán vị của n. Ví dụ cụ thể, giai thừa của 5 bằng 5x4x3x2x1 = 120.
Quay lại với đề bài ban đầu của: Chúng ta có 3 quả bóng, vậy số hoán vị của 3 quả bóng (sau thực hiện phép tính giai thừa) sẽ là:
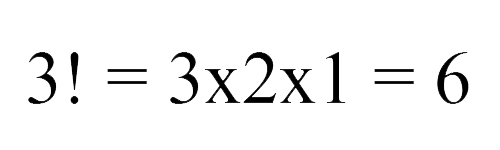
2. ĐỊNH HƯỚNG (CHIỀU/HƯỚNG)
Bây giờ chúng ta xem xét định hướng. 3 quả bóng 3 màu ở đề bài nêu trên không có định hướng bởi vì nó không thể lật hoặc xoay.
Vì vậy, chúng ta chuyển sang vật thể khác có thể lật hoặc xoay. Chọn 3 đồng tiền xu có 2 mặt (sấp-ngửa). Đề bài yêu cầu, sắp xếp 3 đồng xu theo một hàng, nhưng mỗi đồng xu phải được sắp xếp sao cho ít nhất một mặt sấp [hoặc ngửa] hướng lên trên.
Lời giải:
Chúng ta có 3 đồng xu, và mỗi đồng xu có 2 hướng/mặt khác nhau. Số hướng cho 1 hoán vị của đồng xu được tính bằng 2 lũy thừa 3:
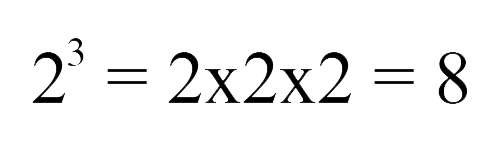
Tiếp theo, ta tính cách sắp xếp 3 đồng xu thỏa mãn yêu cầu đề bài bằng cách nhân số lượng hoán vị với số lượng định hướng, ta có:
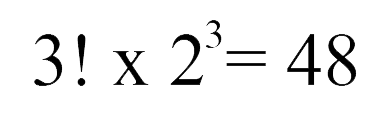
Như vậy 3 đồng xu (có 2 mặt) có thể có 48 cách sắp xếp khác nhau.
3. CÂU CHUYỆN CỦA KHỐI LẬP PHƯƠNG RUBIK 3×3×3
Để tính toán tất cả các hoán vị có thể có của khối Rubik, chúng ta phải biết cơ chế và thiết kế của khối lập phương Rubik.
Khối lập phương Rubik có 6 cạnh và mỗi cạnh chứa 9 hình vuông. Gồm 3 phần chính là trung tâm, góc và cạnh. Có tổng cộng 6 ô trung tâm, 8 góc và 12 cạnh. Tâm của khối được cố định và không thể xoay hoặc định hướng, chúng quyết định màu sắc của mỗi mặt. Các góc và cạnh có thể được xoay đến những hướng khác trong khối.

Để biết khối Rubik 3x3x3 vì sao có đến 43.252.003.274.489.856.000 hoán vị, hãy vận dụng các kiến thức về hoán vị và định hướng (nêu ở phần trên) để giải quyết bài toán này:
Ta có một vật có n hoán vị với p là hướng, cách sắp xếp của vật được tính bằng công thức:
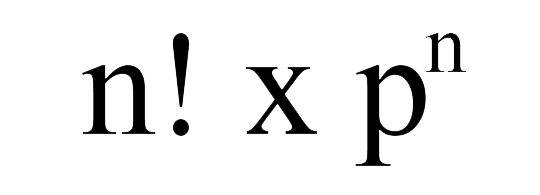
a. Xét vị trí trung tâm của khối Rubik
Phần trung tâm là một phần của trục cố định không di chuyển. Tất cả các ô khác di chuyển xung quanh các ô trung tâm. Điều này có nghĩa là các ô trung tâm có một hoán vị và một hướng.
Do đó, ta có:
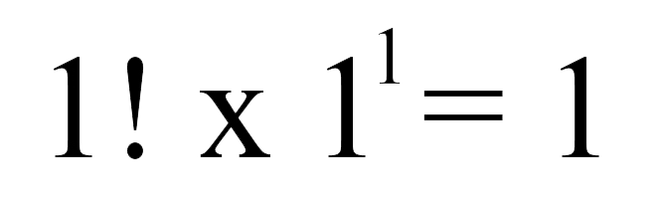
b. Xét vị trí góc của khối Rubik
Khối Rubik có 8 góc. Không giống như ô trung tâm, các ô góc có thể xoay/di chuyển. Vì Rubik có 8 góc nên tổng số hoán vị của các góc là 8!
Để tìm ra hướng cho mỗi góc, chúng ta cần đếm số lượng của màu sắc sơn trên khối góc. Một góc có 3 màu, vì vậy phải có 3 hướng. Điều này có nghĩa là tổng số hướng cho mỗi góc là 3 mũ 8 (38).
Từ đó, ta có thể tính tổng số vị trí cho các góc:
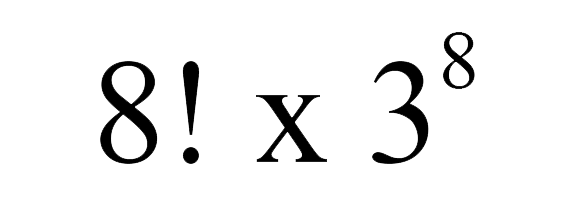

c. Xét vị trí cạnh của khối Rubik
Lập phương Rubik có 12 cạnh và mỗi cạnh có thể di chuyển hoặc lật. Mỗi cạnh có 2 màu sắc, đồng nghĩa với việc có 2 hướng.
Tương tự cách tính tổng số vị trí của 8 góc, ta có tổng số vị trí của 12 cạnh là:
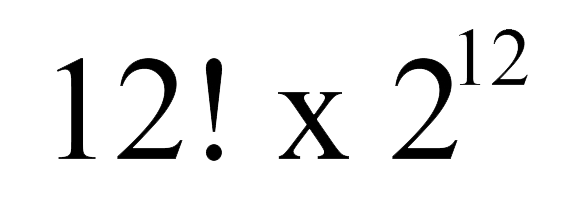

Như vậy, chúng ta đã có tổng vị trí có thể của 6 ô trung tâm, 8 góc và 12 cạnh của một khối Rubik 3x3x3 bằng cách nhân tất cả số mà chúng ta đã tính toán.
Tuy nhiên, do những hạn chế của khối Rubik, nên chỉ có 1 trên 12 vị trí có thể tiếp cận được bằng cách xoay các cạnh của khối. Do đó, phép tính của chúng ta cần chia cho 12.
Do đó ta có:
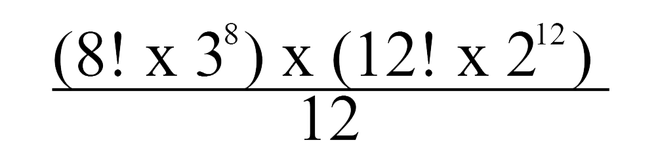
Kết quả: 43.252.003.274.489.856.000
Đọc là: 43 tỷ tỷ 252 triệu tỷ 3 nghìn tỷ 274 tỷ 489 triệu 856 nghìn
Con số này lớn thế nào? Nói một cách hình ảnh, khi sắp xếp chúng (43 tỷ tỷ) thành 1 dãy liên tiếp thì dãy Rubik sẽ dài gần bằng 261 năm ánh sáng. Ngoài ra, hãy tưởng tượng rằng chúng sẽ bao phủ Trái Đất 271 lần nếu xếp số lượng sắp xếp này trải rộng thành bề mặt cong! Bạn có muốn tưởng tượng thêm không? Nếu bạn quay một khối mỗi giây, bạn sẽ cần 1.400 nghìn tỷ năm để quay hết con số hơn 43 tỷ tỷ này!
Ngoài ra, "dân chơi Rubik" sẽ biết đến khái niệm "Con số thần thánh", để chỉ số bước đi nhỏ nhất để giải xong khối Rubik. Từ năm 1981, giáo sư toán học người Mỹ Morwen Thistlethwaite đưa ra con số là 52 bước xoay để giải xong Rubik, tuy nhiên, càng nhiều năm về sau, con số này càng rút ngắn lại. Đến năm 2010, một nhóm các nhà toán học và nhà lập trình máy tính đưa ra con số nhỏ nhất để giải Rubik là 20 và gọi nó là "Con số thần thánh - God's Number".
Một vài con số khổng lồ "gần gũi" với cuộc sống con người:
- Số lượng bit trên đĩa cứng máy tính, tính đến năm 2010: 1013, 500–1000 GB
- Số lượng nguyên tử ước tính trong vũ trụ quan sát được: 1080
- Khối lượng của Trái Đất: 4 × 1051 nucleon
- Số lượng tế bào trong cơ thể người: 3,72 × 1013
- Số lượng các kết nối thần kinh trong não người: 1014
- Số Avogadro chứa trong 12 gram Carbon-12 là: 6,022×1023. [Số Avogadro là số hạt (thường là phân tử, nguyên tử hoặc ion) chứa trong 1 mol].
Bài viết sử dụng nguồn: Number Inception
* Đọc bài cùng tác giả Trang Ly tại đây.