
Phỏng đoán Keller, một bài toán về cách xếp các hình trong không gian, đã được giải gần hết nhưng chỉ còn trong không gian bảy chiều. Nay nhờ sức mạnh tính toán mà các nhà khoa học đã có thể giải quyết phần khó khăn nhất nhưng không thể kiểm chứng bởi con người.
Câu trả lời của máy tính là: Đúng. Nhưng chúng ta không thể khẳng định đáp án này mà chỉ có thể dùng một chương trình máy tính khác để xác minh thuật toán đã nêu trên có đúng hay không. Hãy cùng tìm hiểu thêm.
Phỏng đoán Keller có dạng như sau: "Xếp một không gian n chiều với siêu khối n chiều cùng kích thước sẽ cho ra một cách sắp xếp mà trong đó có ít nhất hai siêu khối với một ‘mặt’ (n-1) chiều chung nhau". Ví dụ như khi những con xúc xắc nằm trong hộp, phía cạnh hộp sẽ chạm vào ít nhất 1 mặt của xúc xắc.
Nhưng với nhiều chiều hơn, mọi thứ trở nên phức tạp. Thuật ngữ siêu khối bao gồm các khối như nhau nhưng có đặc tính không gian khác nhau. Nghĩa là chúng ta không thể phân tích như là với xúc xắc và hộp nữa. Điều này khiến mọi thứ trở nên khó xác định.
"Năm 1986 nhà toán học, khoa học máy tính người Mỹ Nick Szabo đơn giản hóa phỏng đoán Keller xuống nghiên cứu sắp xếp theo thứ tự. Sử dụng kỹ thuật này, Corradi và Szabo giới thiệu giản đồ Keller: giản đồ có các đỉnh mà từng cặp là liền kề nếu và chỉ nếu chúng khác nhau đúng bằng một lượng trong ít nhất một tọa độ và chúng khác nhau trong ít nhất 2 tọa độ".
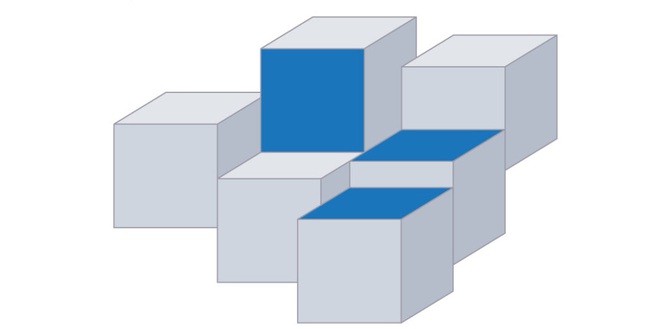
Khi sắp xếp hình khối trong không gian 3 chiều, sẽ có 2 khối chia sẻ một mặt. (Nguồn: Cs.cmu.edu)
Điều này tức là vấn đề, trong không gian bảy chiều, chỉ có thể được giải bằng kỹ thuật "tấn công". Nghĩa là máy tính có thể thử nghiệm tất cả ví dụ để xem xét tính khả thi của từng đáp án. Bài toán có vẻ đơn giản, nhưng tiêu tốn rất nhiều tài nguyên.
Nghĩa là đến một lúc không thể tính toán nữa. Giống như gấp tờ giấy, sau 10 lần gấp tờ giấy đã có ngàn lớp. Giờ hãy tưởng tượng, mỗi lần gập bao gồm các giá trị trục, -10 đến 10. Với 21 giá trị, qua bảy chiều sẽ có 2 tỉ cách kết hợp.
Chứng minh phỏng đoán này mang đến một số bất ngờ. Nhà toán học Oskar Perron đã chứng minh nó đúng từ 1 đến 6 chiều năm 1940. Nhưng vào những năm 1990, Jeffrey Lagarias và Peter Shor chứng minh rằng nó không đúng với 10 chiều.
Bản chất của các chiều cao nghĩa là các nhà toán học có thể tìm đường tắt để giải toàn bộ tập, ví dụ họ có thể chứng minh một một liên kết để phóng lên toàn bộ bài toán.
Chỉ còn chiều thứ 7 là chưa thể giải vì một sự chồng lấn. Sau khi Lagarias và Shor chứng minh, chỉ còn lại chiều 7, 8 và 9. Năm 2002, Mackey chứng minh phỏng đoán này sai trong chiều thứ 8, do vậy cũng sai với 9.
Còn sót lại chiều thứ 7, có thể đây là chiều cao nhất mà phỏng đoán đúng hoặc chiều thấp nhất nơi nó sai. Và bây giờ, máy tính chứng minh phỏng đoán là đúng.

