Những tiêu chuẩn hóa về giấy lần đầu tiên được giới thiệu trong thế kỷ 20 và được gán cho tất cả các nơi trên thế giới cho đến ngày nay. Nhưng sự khác biệt giữa các loại giấy kích thước A khác nhau là gì và chúng đã được chuẩn hóa như thế nào?
Theo ScienceABC, tiêu chuẩn về kích cỡ giấy quốc tế có tên gọi là ISO 216 trong đó xác định kích thước giấy chuẩn quốc tế (ISO) sử dụng ở hầu hết các nước trên thế giới hiện nay.
Nó được dựa trên tiêu chuẩn DIN 476 của Đức cho các khổ giấy. Các tiêu chuẩn ISO phổ biến nhất liên quan đến các loại giấy A, B và C, nhưng trong bài viết này, chúng ta sẽ chỉ đề cập đến biến thể thông dụng nhất: giấy loại A.
Giấy loại A có gì đặc biệt?
Giấy loại A được thiết kế theo cách mà khi bạn cắt đôi chúng, bạn nhận được hai mảnh hoàn toàn giống hệt nhau của giấy loại A tiếp theo. Ví dụ, nếu bạn cắt đôi tờ A0, bạn sẽ có được hai tấm A1 nhỏ; nếu tiếp tục cắt một tờ A1 ra làm đôi, bạn sẽ có trong tay hai tờ A2.
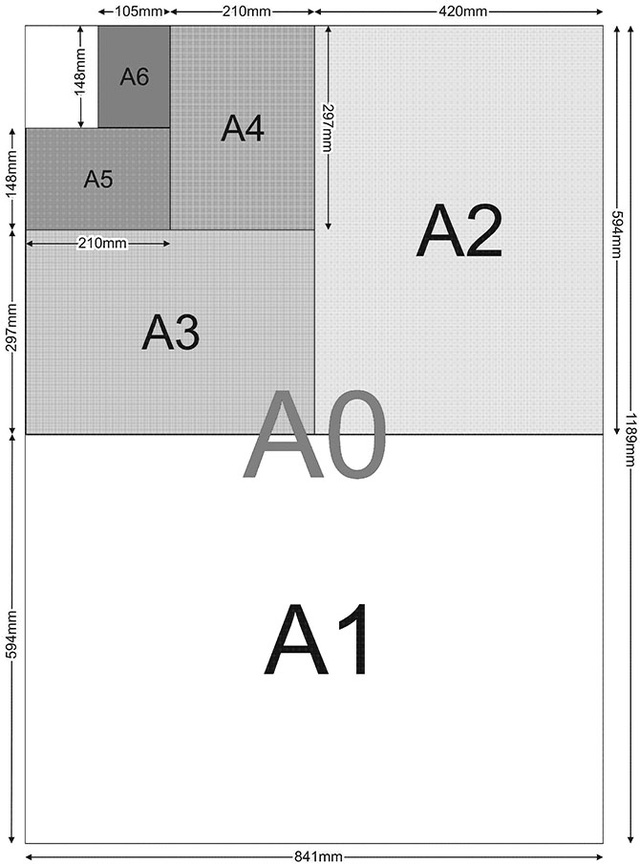
Mặc dù kích thước của hai tờ mới khác nhau so với ‘cha mẹ' của chúng nhưng tỷ lệ chiều dài và chiều rộng của giấy vẫn giữ nguyên. Vì vậy, khi bạn gấp đôi một tờ A3, bạn nhận được hai tờ A4 có cùng tỷ lệ giữa chiều dài và chiều rộng của tờ A3.
Vậy làm cách nào xác định được kích thước chính xác của các tờ giấy loại A này?
Như đã đề cập ở trên, tất cả giấy loại A chuẩn có cùng tỷ lệ giữa chiều dài và chiều rộng. Vậy những giá trị đó nói lên điều gì và làm thế nào tỉ lệ đó không đổi cho tất cả các giấy loại A tiêu chuẩn?
Để trả lời câu hỏi này, chúng ta sẽ phải quay trở lại nơi tất cả bắt đầu: tờ giấy đầu tiên chính thức được chuẩn hóa bằng cách đặt chữ A như một tiền tố với tên của nó là A0.
Một tờ A0 chính xác dài 46,8 inch và rộng 33,1 inch (tương đương 1189*841 mm) và có diện tích 1 mét vuông. Bây giờ, nếu bạn chia 1189 cho 841 (kích thước của một tờ A0) bạn sẽ nhận được con số 1,414. Có gì đặc biệt về con số này? Vâng, đó là kết quả của phép toán khai căn số 2.
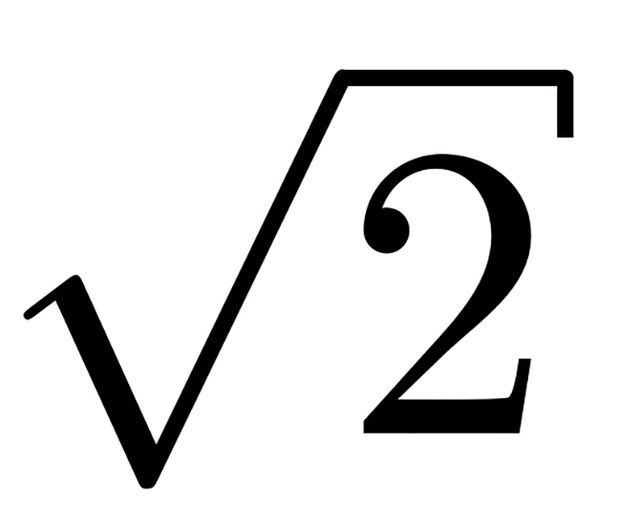
Bạn có thể thấy rằng, cho dù đó là một tấm A8 hoặc một tờ A0, tỷ lệ 1,414 giữa chiều dài và chiều rộng vẫn giữ nguyên. Vẻ đẹp của sự phân biệt rõ ràng như vậy giúp bạn có thể dễ dàng tăng hoặc giảm nội dung như hình ảnh, văn bản… sang những kích thước khác mà không làm mất tính đối xứng.
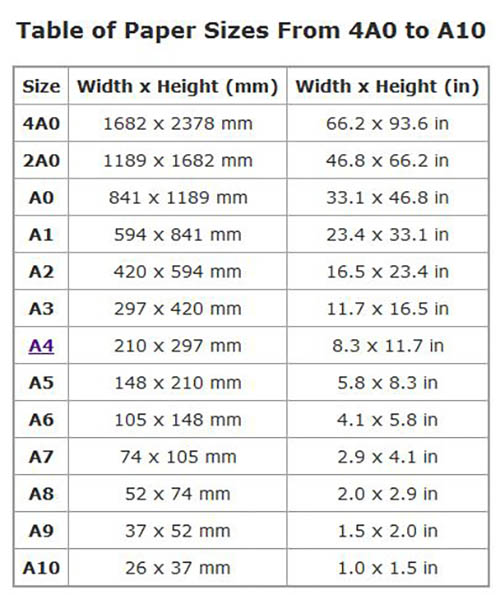
Nếu tỷ lệ giấy A tiêu chuẩn không được cố định, chuyển nội dung từ một kích thước khác sẽ không đơn giản và linh hoạt như vậy. Bởi vì tỷ lệ các cạnh là 1,414, bạn có thể dễ dàng mở rộng một tài liệu sang kích thước lớn nhất tiếp theo lên 141% trên máy.
Mẹo này có ích khi làm việc trên các công cụ chỉnh sửa hình ảnh khác nhau, photocopy tài liệu... Ngoài ra, bạn có thể dễ dàng chuyển đổi kích thước lớn hơn sang hai tờ giấy nhỏ hơn. Chẳng hạn, bạn có thể chia một tấm A2 thành hai tờ A3 đối xứng, hai tờ A3 thành bốn tờ A4 đối xứng,…

Đây là một tiêu chuẩn đơn giản nhưng đầy khéo léo. Ai có thể nghĩ rằng toán học có thể được sử dụng để tạo ra một tiêu chuẩn chung cho kích thước của các loại giấy trên toàn thế giới cơ chứ?