Khi chúng ta nhìn lên bầu trời, không gian trông có vẻ như mở rộng về mọi phía. Đó chính là mô hình tâm trí sơ khai của con người về vũ trụ, nhưng điều đó không thực sự chính xác. Thậm chí đã từng có thời gian chúng ta còn nghĩ rằng Trái Đất là một mặt phẳng!
VŨ TRỤ BAO LA RỘNG LỚN CỦA CHÚNG TA CÓ HÌNH GÌ?
Sở dĩ có điều đó là do so với con người, Trái Đất quá to lớn khiến độ cong của nó gần như là bằng không (giống như một mặt phẳng) khi con người quan sát bằng mắt thường và rất khó để phát hiện ra sự thật rằng Trái Đất là một khối hình cầu.
Mở rộng hơn, vậy hình dạng của vũ trụ là hình gì? Đây quả là một câu hỏi hóc búa mà không phải ai cũng có thể trả lời được.
Để có thể trả lời được câu hỏi này thì chúng ta phải xét trên cả hai phương diện: Một là khía cạnh hình học (góc và diện tích...) và khía cạnh còn lại là topo (cấu trúc liên kết giữa các thành phần trong một hệ).
Những bằng chứng về vũ trụ học (cosmology - là khoa học nghiên cứu tổng thể về vũ trụ) cho thấy vũ trụ quan sát được là một không gian đồng nhất và trơn. Kết cẩu địa phương của không gian cũng tương đồng với mỗi điểm và mỗi hướng.
Chỉ có 3 hình học tương thích với những mô tả này, đó là hình học phẳng, hình học hình cầu và hình học hình học hyperbol. Trong đó, hình học phẳng chính là hình học Euclid mà chúng ta được học ở phổ thông, hai hình học còn lại gọi là hình học phi Euclid.
Hãy lần lượt xét cả 3 hình học trên (về hình học, topo và bằng chứng vũ trụ học) để xem liệu hình học nào sẽ mô tả tốt nhất vũ trụ của chúng ta.
HÌNH HỌC PHẲNG
Đây là hình học cơ bản mà chúng ta được học khi còn là học sinh nhằm mô tả không gian ba chiều mà theo đó tổng 3 góc của 1 tam giác bằng 180 độ và diện tích hình tròn là πr2 và một ví dụ cụ thể nhất cho hình học này chính là mặt phẳng 3 chiều (không gian euclid).
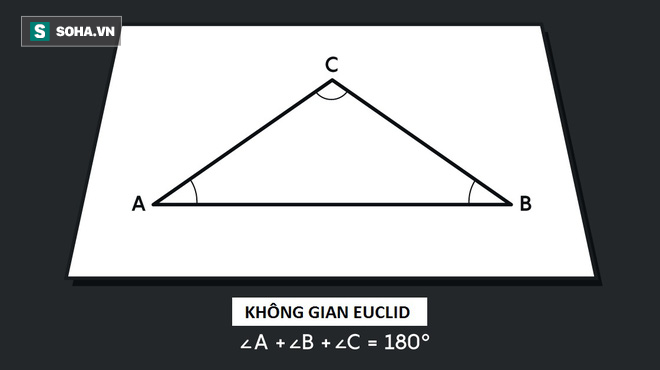
Không gian Euclid. Ảnh: Quantamagazine
Không gian này hơi khó để hình dung nhưng chúng ta có thể xây dựng một vài hiểu biết qua trực giác bằng việc nghĩ về không gian hai chiều thay vì ba. Hãy tưởng tượng một phần mặt phẳng là một tờ giấy và bạn có thể uốn cong để mép này trùng khớp mép kia.
Khi đó, chúng ta sẽ có một hình trụ như hình dưới đây:
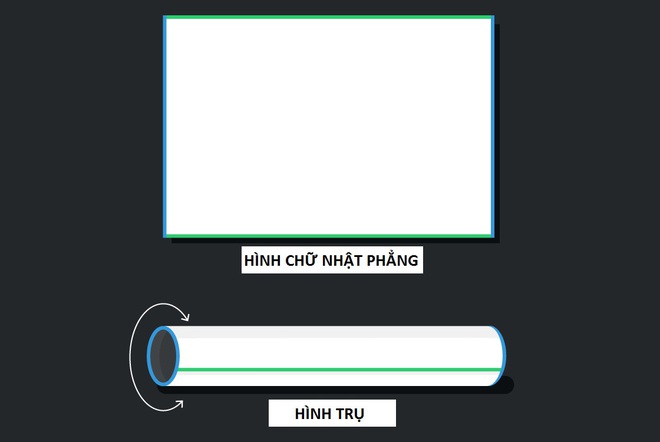
Uốn cong mặt tờ giấy để được 1 hình trụ. Ảnh: Quantamagazine
Tiếp theo, hãy uốn cong hình trụ này để hai đầu có thể chạm nhau và lúc đó bạn sẽ có ngay một chiếc bánh doughnut (trong toán học gọi hình này là hình xuyến), xem ảnh bên dưới.
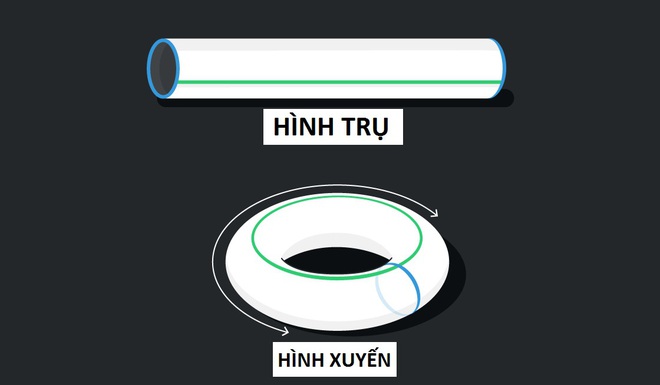
Uốn cong hình trụ để được hình xuyến. Ảnh: Quantamagazine
Bây giờ bạn có thể sẽ nghĩ: "Đây không giống như một mặt phẳng đối với tôi" và thực tế bạn hoàn toàn có lý vì nếu lấy một tờ giấy và làm theo thì bạn sẽ không thể nào ráp hai đầu của hình trụ lại với nhau để được hình xuyến như bên dưới.
Tờ giấy sẽ bị cong và nhăn nheo (không trơn) ở phần mép cong bên trong của hình xuyến vì độ cong của phần đường tròn bên ngoài và bên trong của hình xuyến là hoàn toàn khác nhau. Bạn cũng có thể dùng một vật liệu nào đó co giãn và đàn hồi hơn tờ giấy.
Thế nhưng điều đó có nghĩa là bạn đã làm thay đổi (bóp méo) độ dài và góc, nghĩa là thay đổi yếu tố hình học của nó. Thực tế thì trong không gian ba chiều, không có bất cứ cách nào để xây dựng một hình xuyến vật lý trơn từ một mặt phẳng mà không làm bóp méo mặt phẳng đó.
Tuy nhiên, ví dụ trên sẽ giúp bạn hình dung về việc sống trong một không gian ba chiều sẽ như thế nào (trong đó bạn là một sinh vật sống trong một mặt phẳng hai chiều và mặt phẳng đó lại nằm trong một hình xuyến ba chiều).
Hãy tưởng tượng bạn là một sinh vật hai chiều và vũ trụ là một hình xuyến với hình học của vũ trụ này được tạo nên từ một miếng giấy phẳng, tức những gì chúng ta biết về hình học phẳng đều đúng (tổng 3 góc tam giác là 180 độ...).
Thế nhưng sự thay đổi topo chúng ta tạo nên từ việc cắt và nối tờ giấy lại nghĩa là những trải nghiệm cuộc sống trên không gian mới này là rất khác biệt so với trước kia. Ví dụ như đường thẳng ở mặt phẳng sẽ trở thành các đường cong như hình dưới.
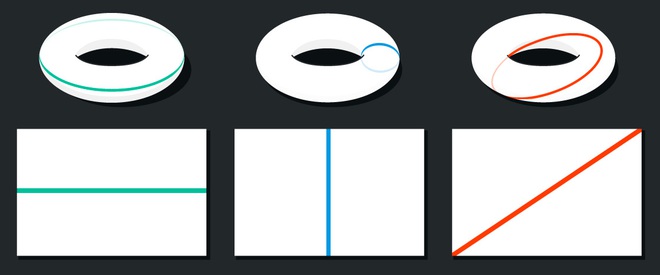
Đường thẳng tương ứng trong mặt xuyến và mặt phẳng. Ảnh: Quantamagazine
Nghĩa là nếu ở vũ trụ hình xuyến, đường truyền của ánh sáng có thể bị bẻ cong và bạn thậm chí có thể nhìn thấy chính mình khi nhìn theo hướng của những đường thẳng trên.
Thật thú vị phải không nào?
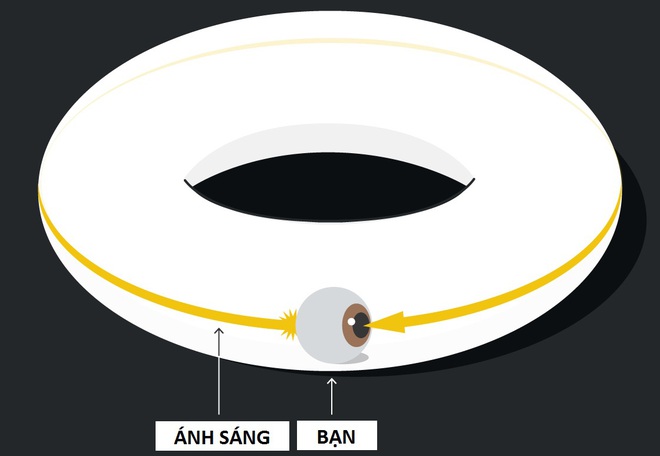
Bạn sẽ nhìn thấy cái lưng của mình trong vũ trụ hình xuyến. Ảnh: Quantamagazine
Còn trong thế giới hai chiều của tờ giấy, ánh sáng đi từ phía sau bạn sẽ đi tới mép giấy bên trái và sau đó xuất hiện ở phía bên phải gần như ngay lập tức. Nói cách khác, ánh sáng trở về đúng nơi mà nó xuất phát.
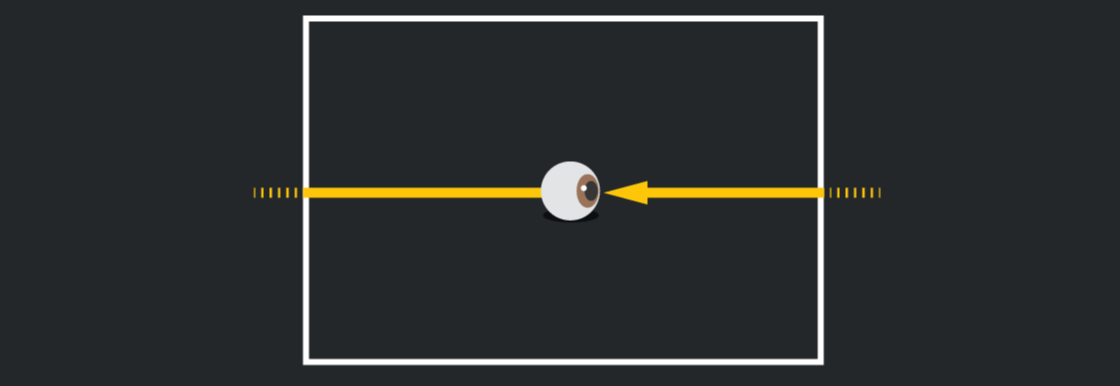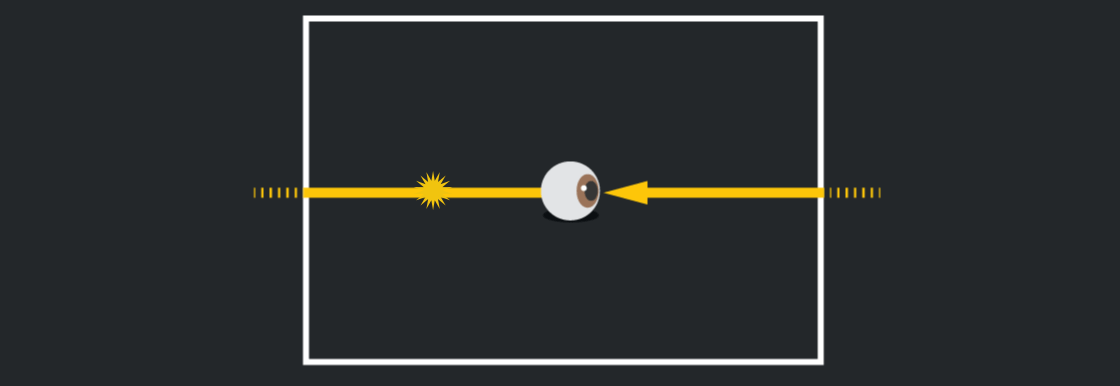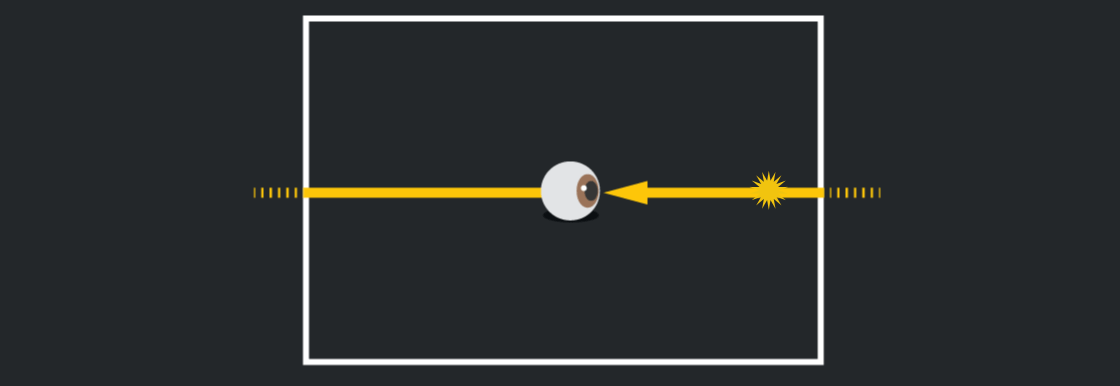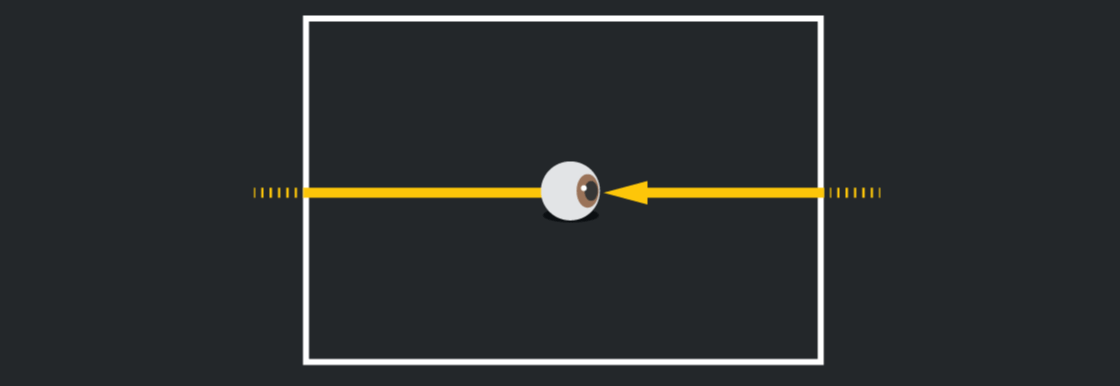
Ánh sáng truyền tới bạn trong mặt phẳng. Ảnh: Quantamagazine
Bạn cũng có thể hình dung mình đi tới một trong 1 mép giấy, sau đó biến mất và xuất hiện trong một "căn phòng" mới nhưng thực ra là cùng một phòng. Tức là trong vũ trụ này, bạn có thể đi tới vô hạn căn phòng giống hệt căn phòng ban đầu mình đứng.
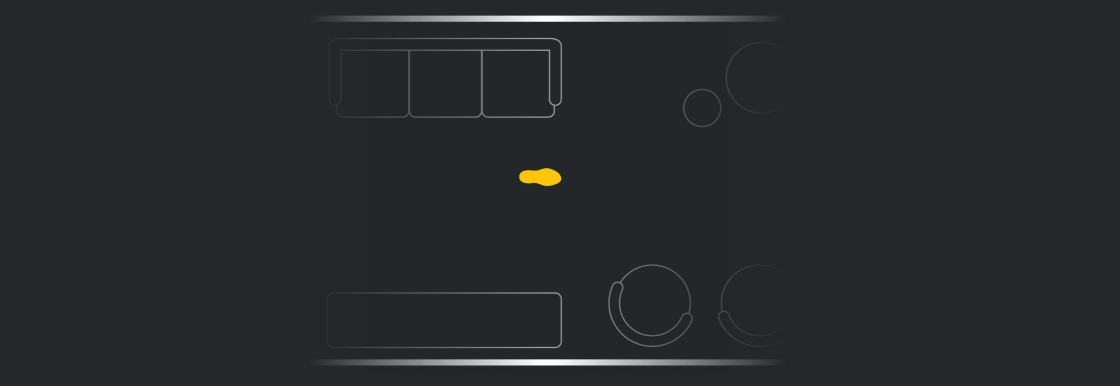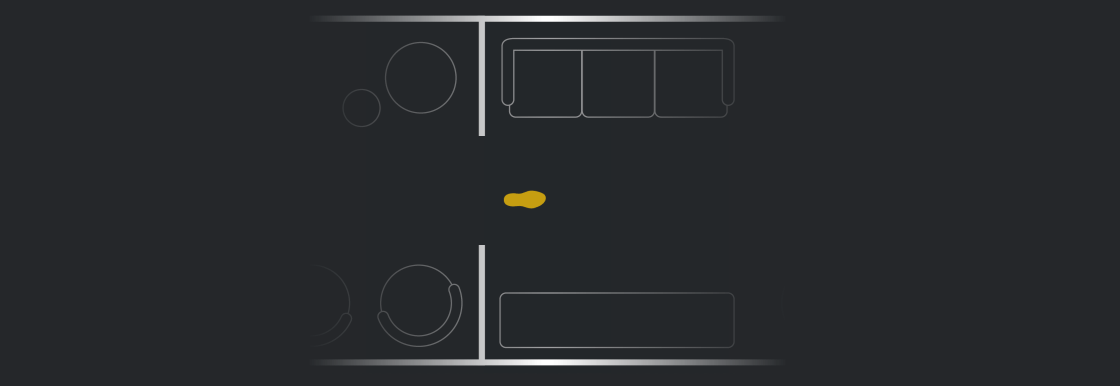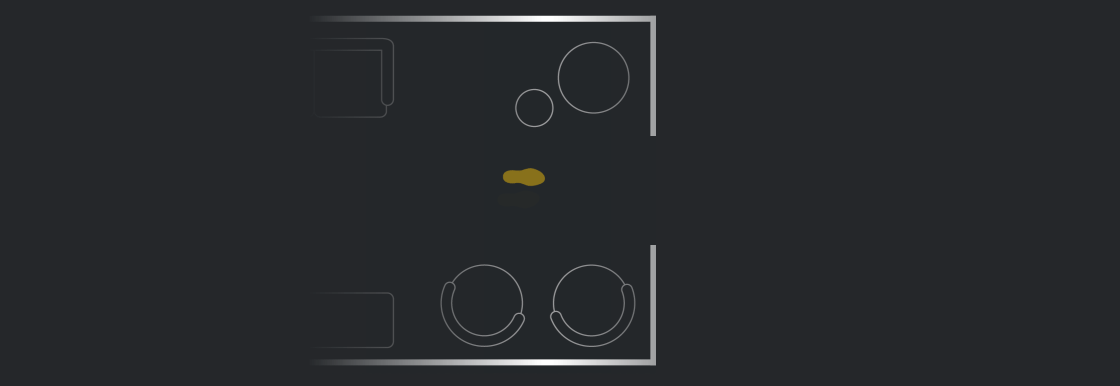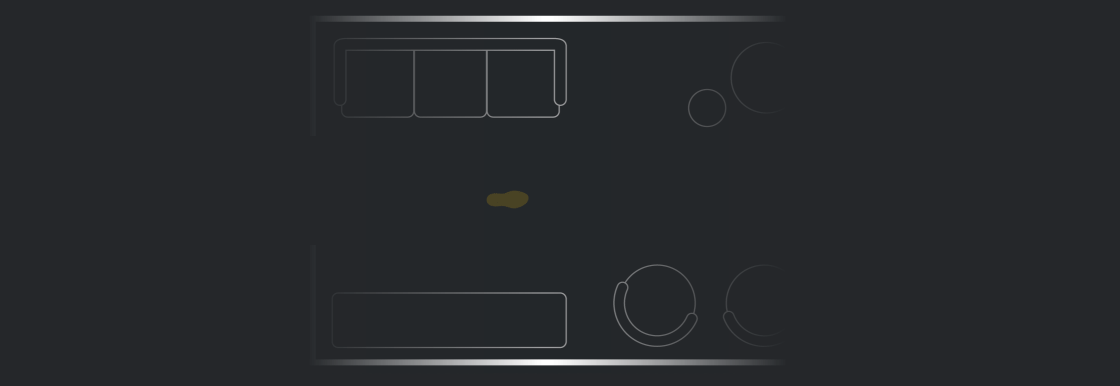
Bạn có thể đi tới vô hạn căn phòng giống hệt căn phòng ban đầu mình đứng. Ảnh: Quantamagazine
Điều này còn có nghĩa là bạn cũng có thể nhìn thấy vô hạn những bản copy của chính mình khi nhìn theo những hướng khác nhau, gọi là hiệu ứng "phòng gương" (hall-of-mirrors effect).
Xem ảnh dưới:
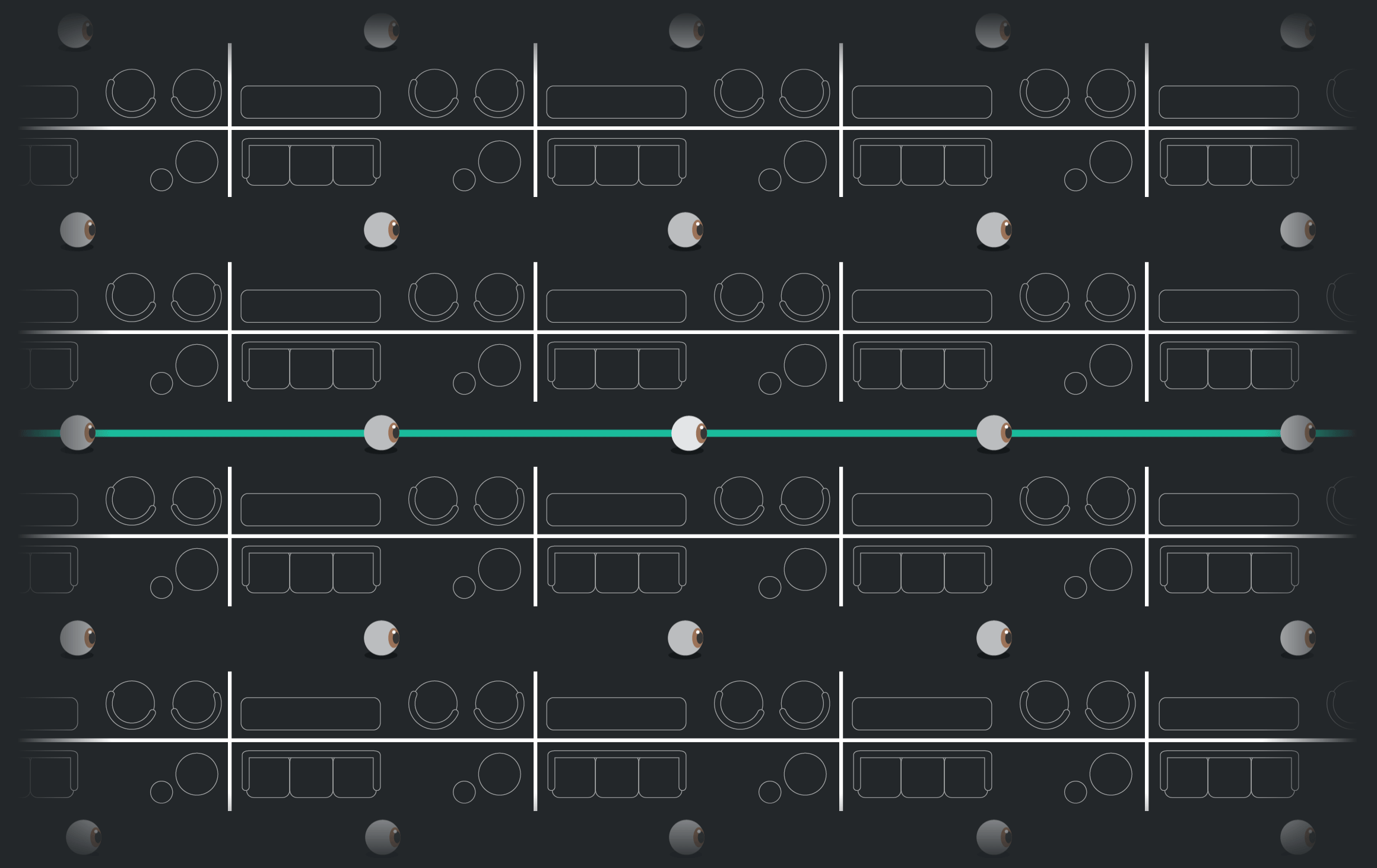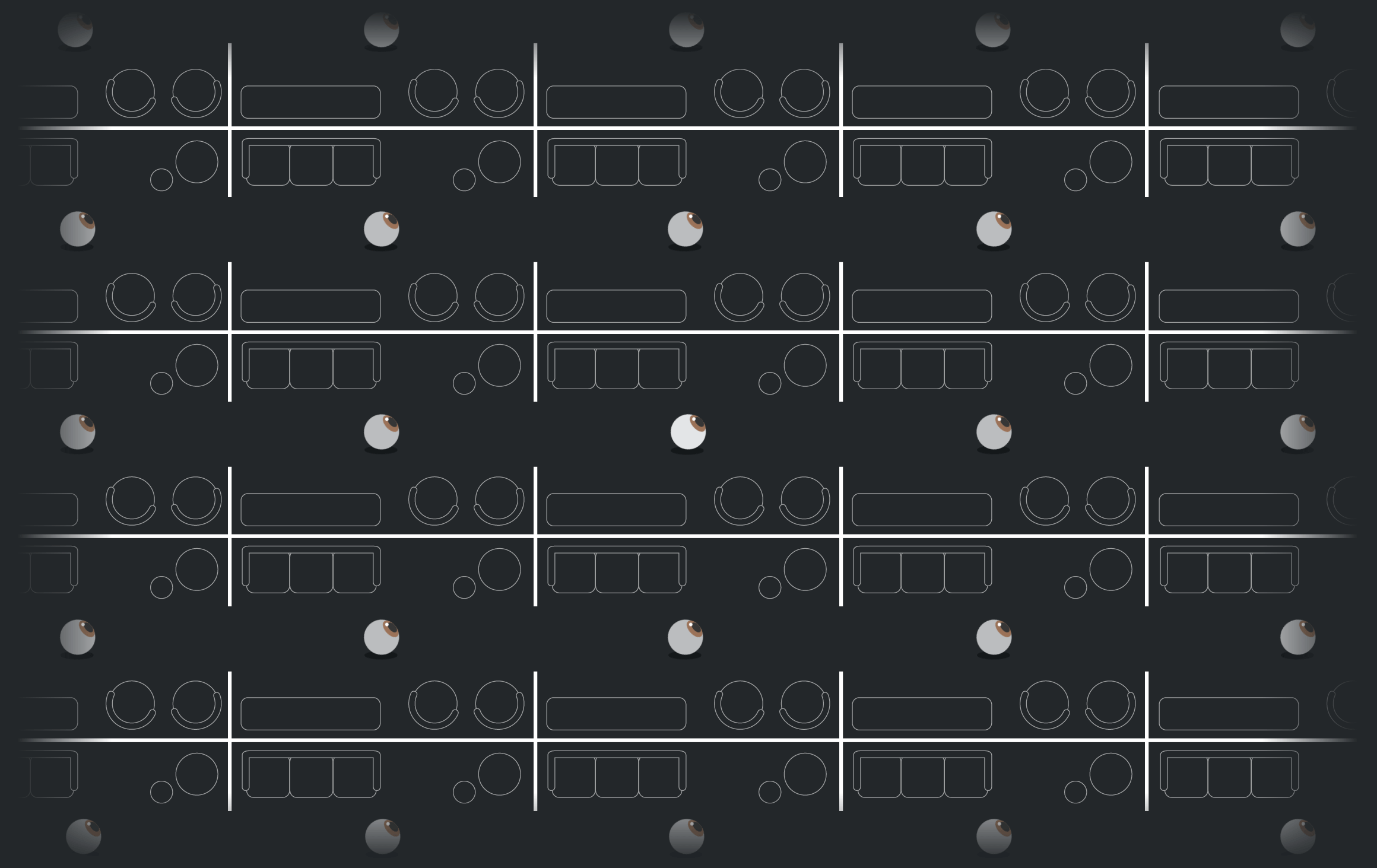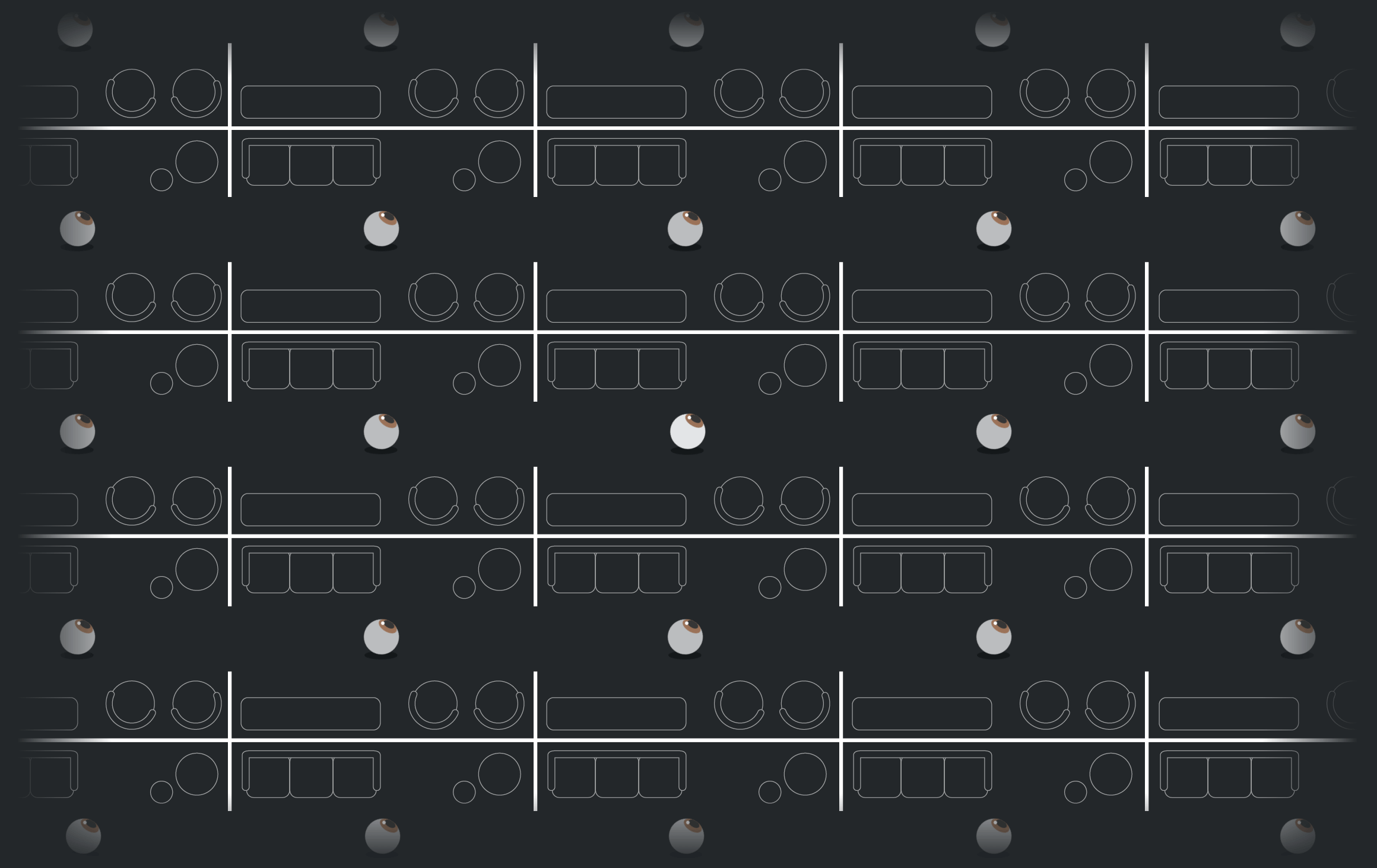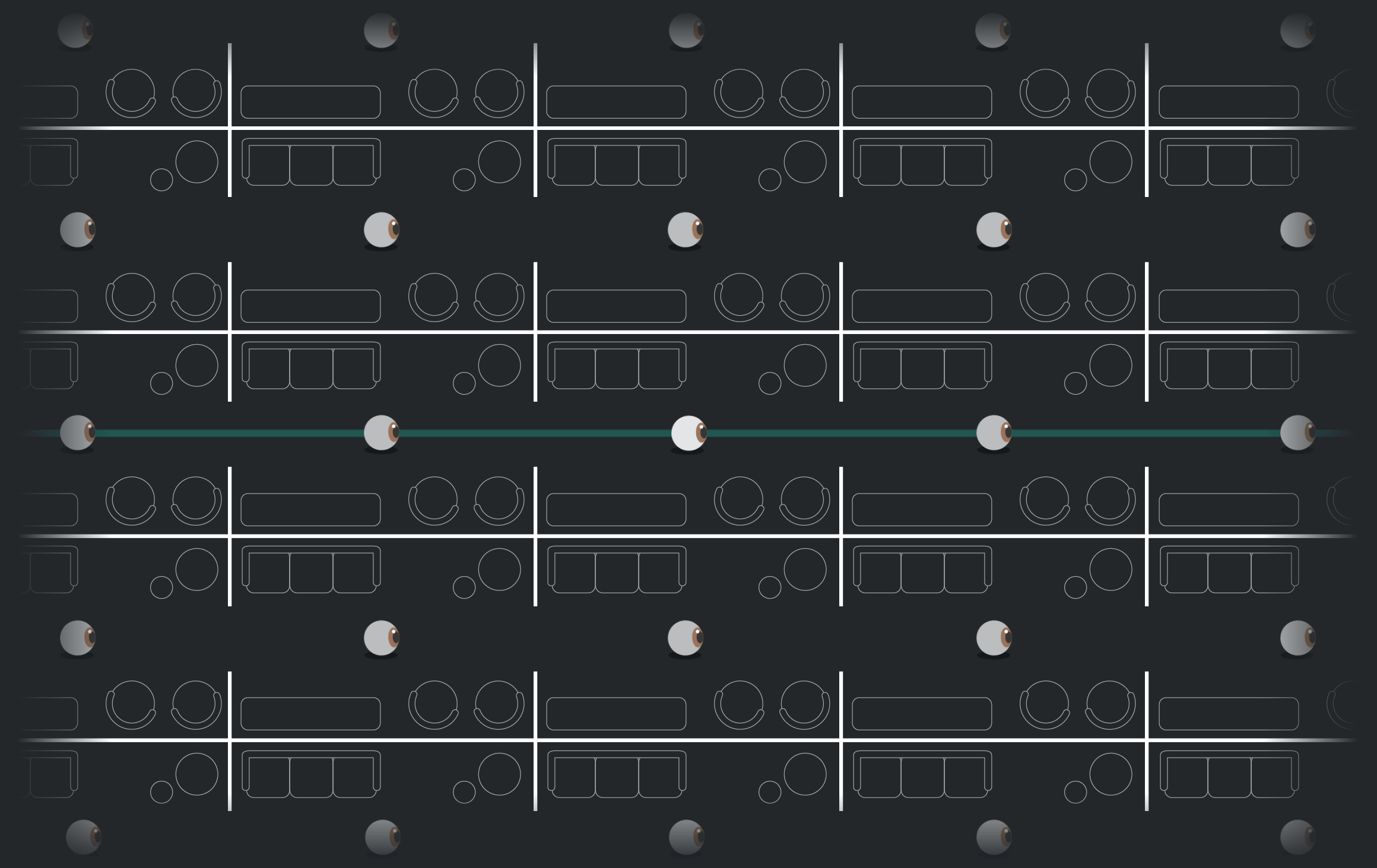
Hiệu ứng " phòng gương". Ảnh: Quantamagazine
Trong vũ trụ hình chiếc bánh doughnut, những điều này tương ứng với nhiều vòng khác nhau mà theo đó ánh sáng có thể đi từ phía trước bạn đến phía sau lưng.
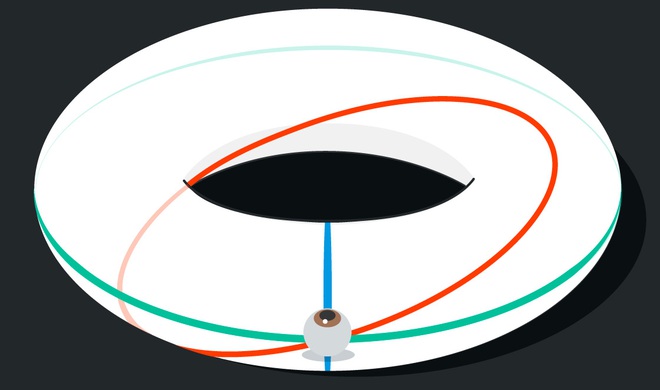
Ánh sáng truyền đi theo 1 đường cong khép kín. Ảnh: Quantamagazine
Tương tự, chúng ta có thể xây dựng nhiều vũ trụ hình xuyến ba chiều như vậy bằng cách dán những mặt đối diện của một hình hộp lại, khi đó cuộc sống trong không gian hai chiều thuộc hình xuyến cũng giống như các hình chữ nhật xếp cạnh nhau.
Còn cuộc sống trong không gian ba chiều lại giống như các căn phòng hình lập phương giống hệt nhau và bạn cũng sẽ thấy vô số bản copy của mình trong không gian này.

Hiệu ứng gương trong không gian 3 chiều. Ảnh: Quantamagazine
Không gian hình xuyến 3 chiều chỉ là một trong 10 thế giới hữu hạn phẳng khác nhau. Có những thế giới vô hạn có mô hình hóa 3 chiều như hình trụ. Trong mỗi thế giới này là những trải nghiệm "phòng gương" khác nhau.
Có phải vũ trụ của chúng ta là một trong những hình phẳng này?
Khi chúng ta nhìn vào không gian, chúng ta không thể thấy những vô số bản thế của chính mình. Thế nhưng thật khó để kết luận rằng vũ trụ không thuộc 1 trong số những hình dạng phẳng này.
Có một điểm chung giữa chúng, đó là tất cả không gian này đều có tính chất hình học giống với không gian Euclid và nếu bạn không thấy bản sao của chính mình thì những hình ảnh ở xa mà bạn thấy (thiên hà, ngôi sao, lỗ đen...) lại cho thấy quá khứ xa xôi.
Sở dĩ bây giờ bạn có thể nhìn thấy quá khứ vì tốc độ ánh sáng tuy rất nhanh nhưng lại hữu hạn và nó phải mất một thời gian dài mới có thể truyền đến bạn. Do đó, có thể chúng ta đang nhìn thấy một bản sao không thể nhận ra ở ngoài kia.
Hay những bản copy của bạn lại khác nhau tùy thuộc khoảng cách đến bạn và chúng quá xa để bạn có thể nhìn thấy (do vũ trụ quá rộng lớn và bạn không thể sống mãi để có thể nhìn thấy điều kỳ diệu này).
Bằng chứng vũ trụ học
Thực tế, các nhà thiên văn không tìm kiếm bản sao này mà thay vào đó, họ tìm kiếm những đặc điểm lặp lại ở một nơi xa nhất mà chúng ta có thể thấy: Nền vi sóng vũ trụ (Cosmic Microwave Background - CMB).
Nền vi sóng vũ trụ chính là "tàn dư" của vũ trụ sau vụ nổ Big Bang, điều đó cũng có nghĩa là khi tìm thấy một cặp CMB tương ứng với hai điểm nóng và điểm lạnh thì có thể dự đoán chúng thuộc cùng một vòng tròn khi nhìn từ hai hướng khác nhau.
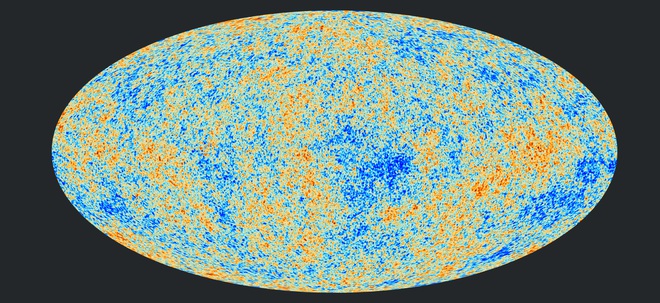
Hình ảnh của bức xạ nền vi sóng vũ trụ, được chụp bởi vệ tinh Planck của Cơ quan Vũ trụ Châu Âu (ESA) vào năm 2013, cho thấy những dao động nhỏ trên bầu trời Credit: ESA/Planck Collaboratio
Tuy nhiên, đến năm 2015 thì các nhà thiên văn đã sử dụng kính viễn vọng không gian Planck của Cơ quan Vũ trụ Châu Âu (ESA) để chụp lại bức ảnh có độ chính xác cao nhất của CMB, tuy vậy sự biến động của CMB ở các thang góc lớn không phù hợp với dự đoán.
Các nhà khoa học đã thất bại trong việc tìm kiếm "bản sao" nhưng điều đó cũng có thể là do vũ trụ của chúng ta quá lớn và những "bản sao" ấy nằm ngoài vũ trụ quan sát được (vùng không gian mà con người có thể quan sát được bằng các thiết bị khoa học hiện đại nhất).
Lưu ý: Đường kính vũ trụ quan sát được là khoảng 93 tỷ năm ánh sáng và đó chỉ là phần nổi trong "tảng băng chìm" là phần vũ trụ không quan sát được.
HÌNH HỌC HÌNH CẦU
Hình học hình cầu cũng tương tự với hình cầu hai chiều như bề mặt quả cam, quả bóng hay Trái Đất. Nhưng điều đó sẽ có nghĩa như thế nào đối với vũ trụ của chúng ta nếu nó là một khối cầu ba chiều?
Tương tự như ở hình học phẳng, chúng ta có thể sử dụng phép suy luận loại suy hay phép tương tự để hình dung vấn đề. Hãy bắt đầu bằng mặt cầu 2 chiều (bao gôm tập hợp tất cả các điểm cách đều 1 điểm gọi là tâm mặt cầu).
Đây là hình ảnh mặt cầu hai chiều thông thường trong không gian ba chiều, tương tự một hình cầu 3 chiều trong không gian 4 chiều cũng sẽ là tập hợp những điểm cách đều 1 điểm.
Sự sống trong không gian hình cầu ba chiều sẽ rất khác so với không gian hình cầu hai chiều, chúng ta đang sống trên bề mặt Trái Đất cũng là một ví dụ cụ thể nhất cho việc sống trong một không gian hình cầu hai chiều.
Chúng ta khó lòng có thể cảm nhận chiều không gian hình cầu 3 chiều của vũ trụ, trong không gian đó ánh sáng truyền đi theo đường ngắn nhất và là một đường tròn lớn và đối với chúng ta thì đường tròn lớn đó lại như một đường thẳng.
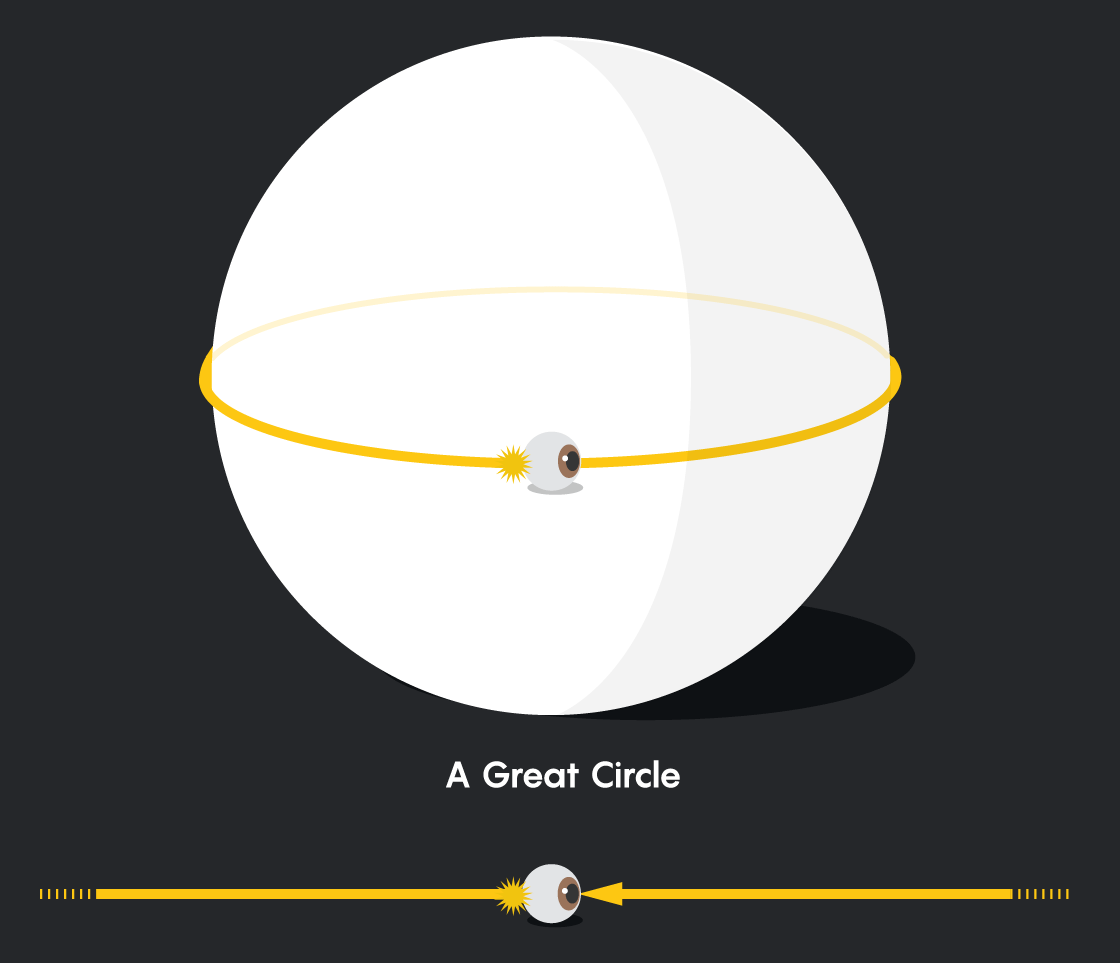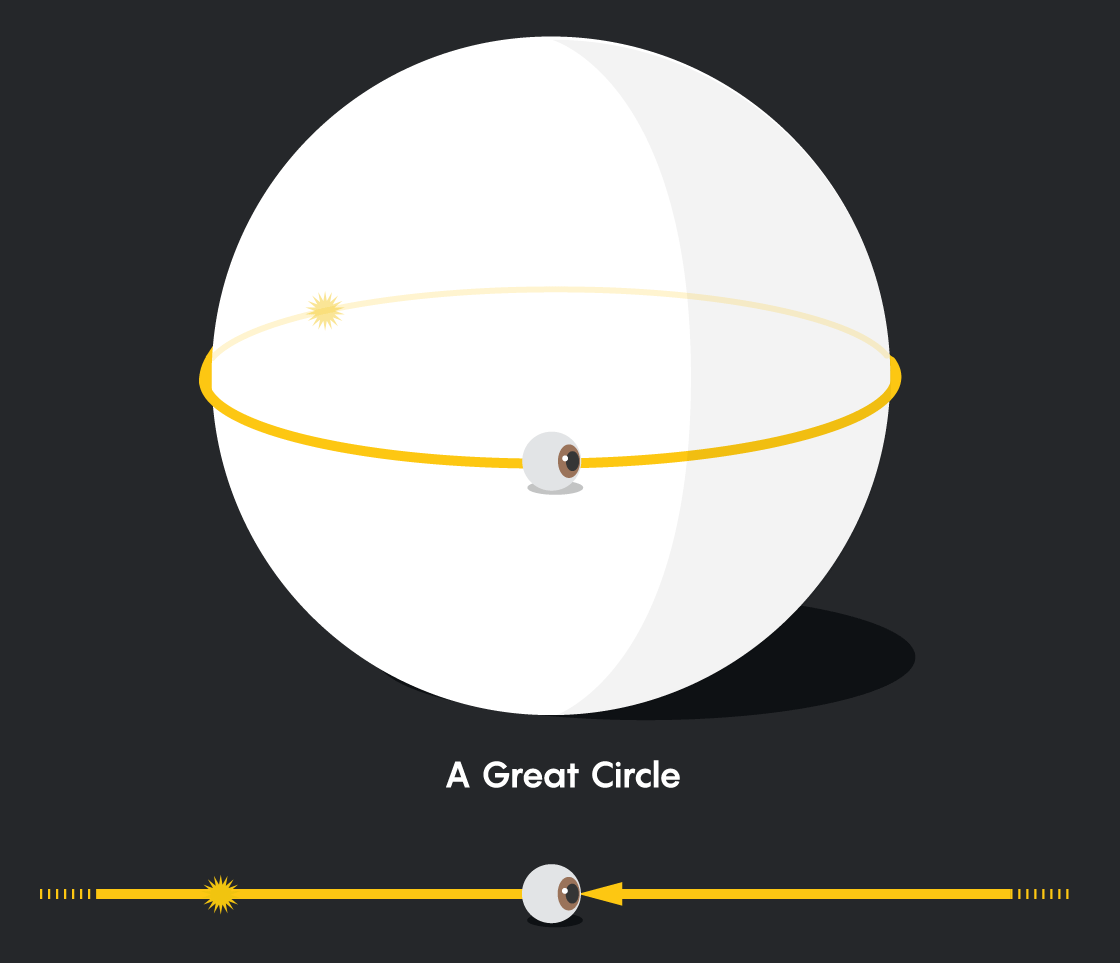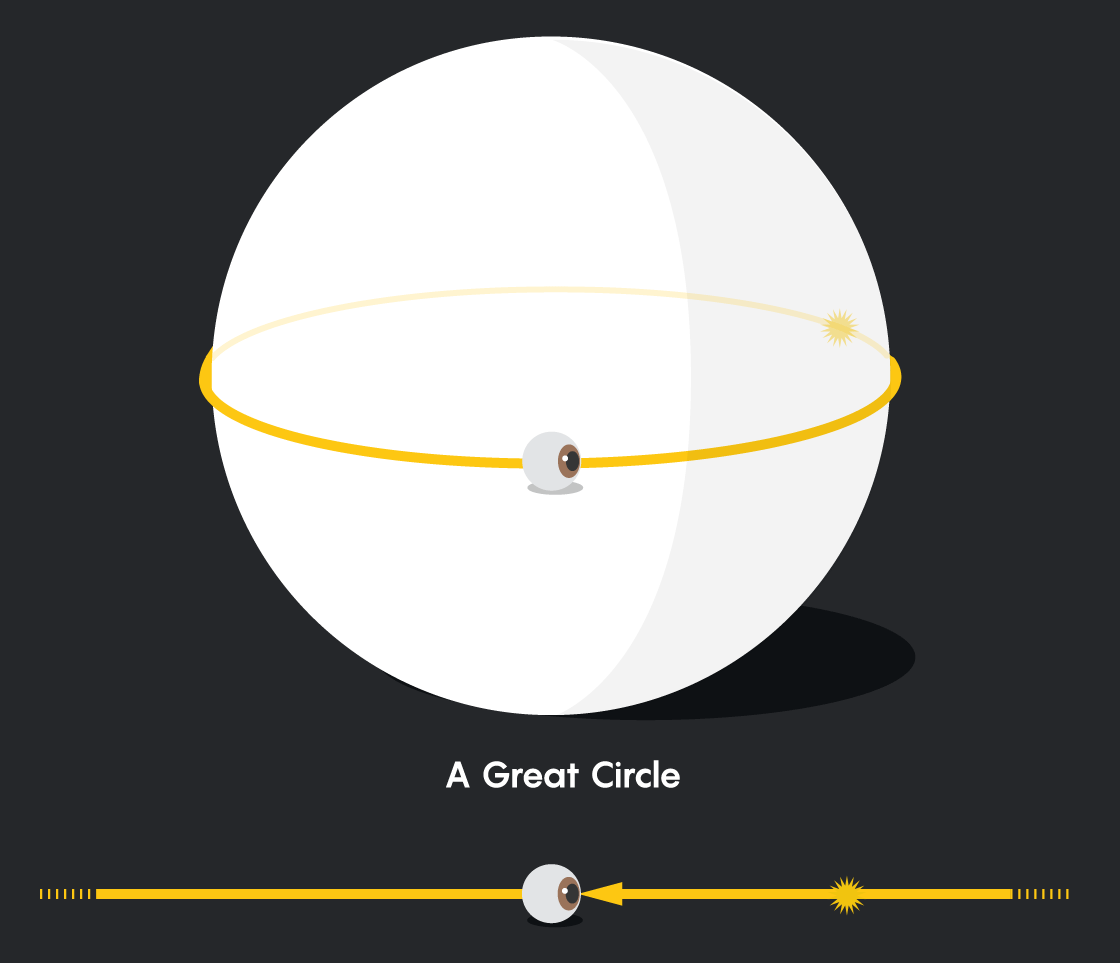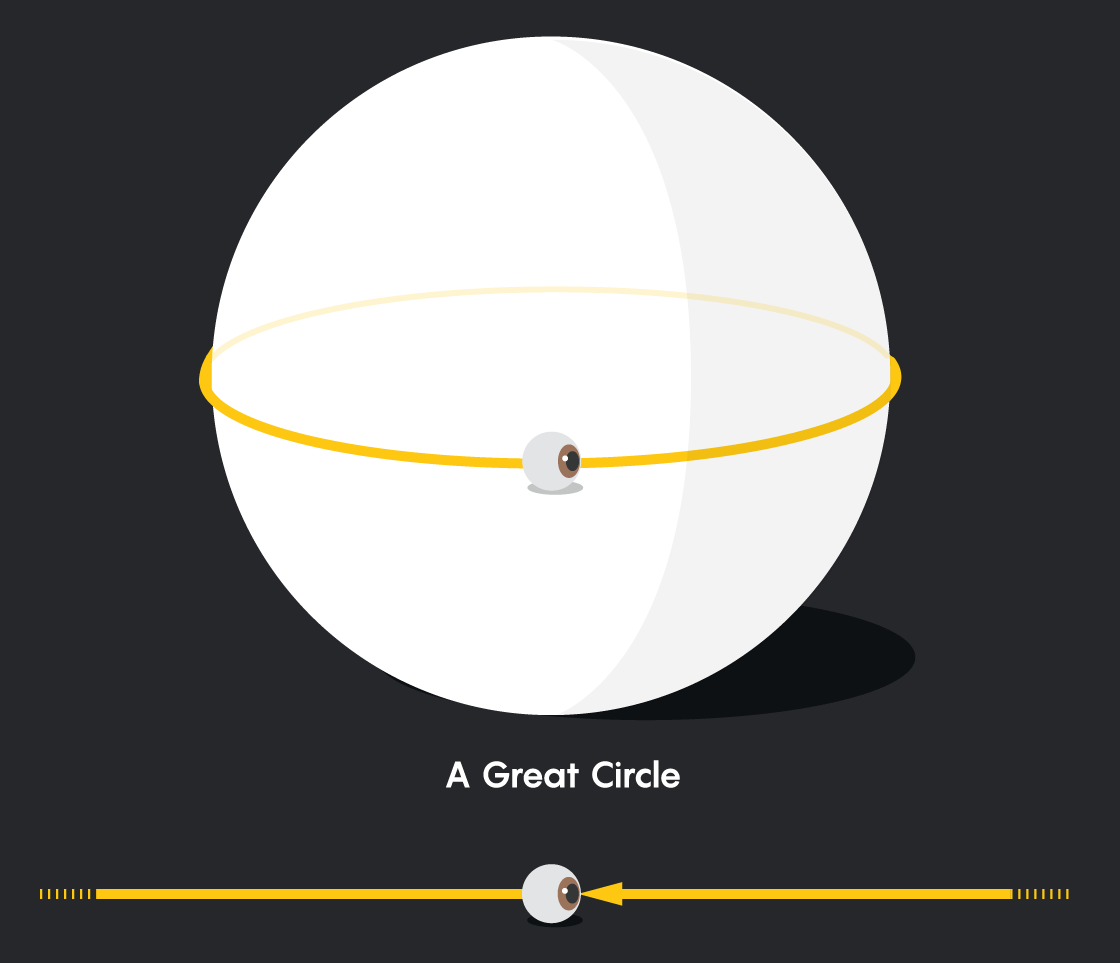
Ánh sáng truyền đi trong không gian mặt cầu. Ảnh: Quantamagazine
Bạn có thể hiểu nó một cách dễ dàng như sau, khi bạn đứng trên mặt đất và thấy một ánh sáng từ phía xa. Bạn cho rằng ánh sáng đi theo 1 đường thẳng từ nguồn sáng tới mắt mình, thế nhưng sự thật thì đường truyền đó lại là một đường cong (theo bề mặt Trái Đất).
Dễ hiểu hơn, giả sử bạn đang ở 1 địa điểm A và muốn đi tới địa điểm B, bạn đi theo đường thẳng ngắn nhất tới điểm đích nhưng thật ra quãng đường bạn đi lại là một đường cong vì bề mặt Trái Đất là hình cầu.
Xem ảnh dưới:
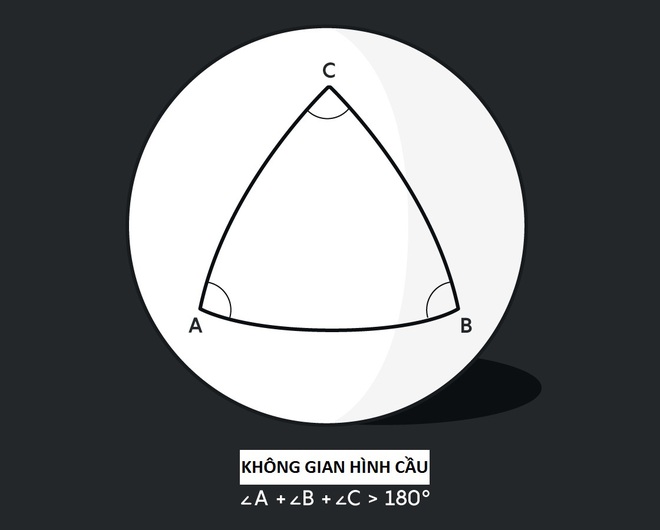
Tổng 3 góc tam giác lớn hơn 180 độ. Ảnh: Quantamagazine
Những đoạn thẳng AB, AC, BC vốn được cho là đường thẳng đối với chúng ta trên mặt đất thì thực ra lại là những đường cong và một hệ quả quan trọng đó là tổng ba góc trong tam giác sẽ lớn hơn 180 độ.
Từ đó có thể thấy khi ánh sáng truyền đi theo một đường tròn khép kín như vậy thì bạn có thể nhìn thấy chính mình khi ánh sáng quay trở về nơi xuất phát.
Như vậy trên không gian mặt cầu chúng ta vẫn có hiệu ứng "phòng gương" tương tự như trên không gian phẳng, chỉ có điều số "căn phòng" để đi qua là hữu hạn thay vì vô hạn như ở không gian phẳng.
Vậy có phải vũ trụ là một hình cầu?
Giống như không gian phẳng, chúng ta không thể nhìn thấy chính mình nhưng điều đó cũng có nghĩa là không gian hình cầu của vũ trụ là không tồn tại mà là do vòng tròn đó quá lớn (lớn hơn kích thước của vũ trụ quan sát được) nên phải rất lâu nữa chúng ta mới thấy... chính mình.
Bằng chứng vũ trụ học
Thực tế, các nhà khoa học tiến hành đo các tam giác trong vũ trụ để có thể tính được độ cong của vũ trụ thông qua tam giác có hai đỉnh là điểm nóng, điểm lạnh và điểm còn lại chính là Trái Đất, rồi tiến hành đo góc để tính độ cong.
Trong hầu hết các phép đo về độ cong, kết quả cho thấy vũ trụ có độ cong rất nhỏ và gần như là một mặt phẳng nhưng năm 2018. Điều này cũng giống như chúng ta cảm nhận về mặt đất như một mặt phẳng do con người quá nhỏ so với Trái Đất.
Các phép đo bằng kính viễn vọng Planck của 1 nhóm các nhà khoa học lại cho thấy vũ trụ là 1 hình cầu. Mặc dù vậy các nhà nghiên cứu khác vẫn xem đó là sự ngẫu nhiên trong thống kê.
HÌNH HỌC HYPERBOL
Không giống như hình cầu với độ cong lên chính nó, hình học hyperbol lại mở rộng vô hạn về mọi hướng như trong hình học phẳng, đó là hình học của rặng san hô, đèo núi... hay hình đĩa Poincaré dưới đây là một ví dụ tiêu biểu.

Hình đĩa Poincaré. Ảnh: Quantamagazine
Sự mở rộng của không gian hình học hyperbol lại rất khác biệt so với hai không gian chúng ta đã xét đến trước đó. Nếu nhìn những hình trên bạn sẽ nghĩ rằng các tam giác gần biên giới đường tròn sẽ nhỏ hơn tam giác nằm ở bên trong.
Thực tế thi tất cả chúng đều bằng nhau và một điều đặc biệt nữa, đó là tổng 3 góc trong tam giác luôn bé hơn 180 độ.

Tất cả các tam giác đều bằng nhau dù ở gần biên vòng tròn hay ở trung tâm. Ảnh: Mathematic
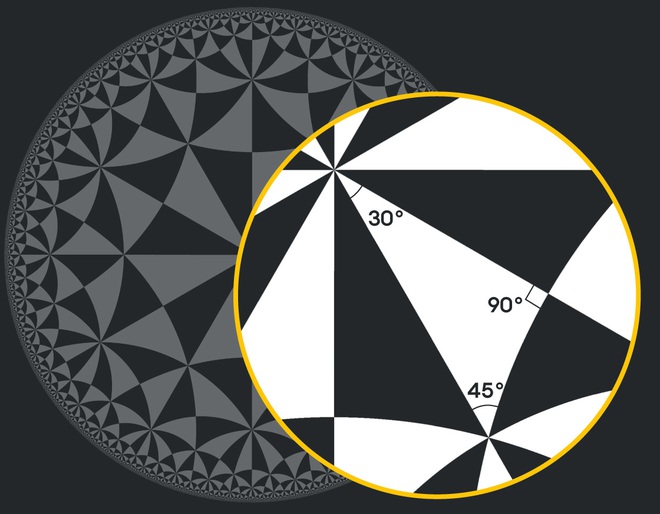
Tam giác trong hình đĩa Poincaré có tổng luôn bằng 165 độ. Ảnh: Quantamagazine
Nhà toán học người Pháp Jules Henri Poincaré (1854 – 1912) lỗi lạc nhất nước Pháp và có lẽ là cả thế giới lúc bấy giờ, đồng tác giả của thuyết tương đối "thu hẹp" và cha đẻ của topo học đã đưa ra giả thuyết mang tên mình nhằm phỏng đoán táo bạo về hình dạng khả dĩ của vũ trụ.
Giả thuyết Poincaré được đề ra năm 1904 đã trở thành bài toán thách thức lớn nhất của toán học thế kỷ 20. Bài toán cũng được Học viện Toán học Clay xếp vào 1 trong 7 bài toán hóc búa chưa có lời giải để thách đố các nhà toán học thế kỷ 21 và đưa ra phần thưởng tới 1 triệu USD.
Vậy liệu có phải vũ trụ có hình hyperbol?
Bài toán tưởng chừng không có lời giải trên đã được thiên tài toán học người Nga lỗi lạc của thế kỷ 21 là Grigori Perelman (sinh năm 1966) giải quyết năm 2002 nhưng vớ cá tính kỳ quặc, lập dị của mình, ông đã từ chối nhận số tiền thưởng 1 triệu USD và cả huy chương Fields...
Tuy nhiên ông lại không đưa ra một công trình đầy đủ về chứng mình của mình trên các tạp chí khoa học ngoài hai bản nghiên cứu dài khoảng 61 trang viết tay. Có tới 3 nhóm chuyên gia hàng đầu làm việc độc lập để kiểm tra công trình phức tạp này.
Người ta không phát hiện ra lỗi nào trong các chứng minh nhưng cũng không có ai dám đứng ra xác nhận công trình này là đúng mà phải đến năm 2006, ba nhóm chuyên gia mới thống nhất rằng cách chứng minh của Perelman là chính xác.
Tuy nhiên, Perelman chứng minh được toàn bộ Giả thuyết Hình học hóa hay chưa nhằm trả lời câu hỏi về hình dáng vũ trụ có lẽ còn phải chờ thêm một thời gian nữa. Do đó, vũ trụ có hình hyperbol vẫn là một đáp án còn bỏ ngõ!

Perelman trình bày cách chứng minh giả thuyết Poincaré tại giảng đường Weaver Hall, đại học New York vào tháng 4/2003 (Ảnh: Frances M. Roberts)
Chúng ta không thể chắc chắn rằng vũ trụ mà chúng ta sinh sống có hình cầu hay hyperbol bởi vì nếu xét trên 1 phần nhỏ của không gian này thì không gian được xét đến gần như là phẳng. Đó cũng là nguyên nhân khiến con người trước kia cho rằng Trái Đất phẳng.
Bài viết được dịch từ các nguồn:
Quantamagazine, sách Giả thuyết Poincaré - Cuộc tìm kiếm hình dạng vũ trụ, Space
