Hãy tưởng tượng nếu bạn muốn đếm số tóc trên đầu tổng thống Trump bằng đôi bàn tay, bạn sẽ cần có nhiều ngón tay hơn, dù tóc tổng thống không có là bao. Chúng tôi không nói rằng bạn CẦN phải làm vậy, nhưng đôi khi việc có thể dùng đôi bàn tay đếm nhiều số lại mang đến khá nhiều tiện ích cho bạn đó.
Tuy nhiên, trên thực tế, bạn không cần phải có nhiều hơn 10 ngón tay, bạn vẫn có thể đếm được đến con số rất rất cao. Vậy hãy cùng Science ABC tìm hiểu xem bạn có thể đếm cao đến mức nào với đôi bàn tay của mình nhé!
Mỗi bàn tay con người có 5 ngón, hay nói chính xác hơn, là bao gồm một ngón cái và bốn ngón tay. Do đó, với cả hai bàn tay, chúng ta rất dễ dàng để có thế đếm đến 10. Trong trường hợp này, không cần đếm theo thứ tự và cũng không cần lấy một ngón tay làm mốc.
Bạn có thể đếm xuôi đếm ngược hoặc đếm lung tung tùy sở thích, miễn là đảm bảo yêu cầu "một ngón tay không được đếm hai lần".
Trình độ nghiệp dư: 24
Hầu hết mọi người thường lợi dụng ba đốt ngón tay để đếm được nhiều hơn. Mỗi đốt được tính bằng một số đếm, một bàn tay có 4 ngón không kể ngón cái làm "công cụ đếm" sẽ cho phép bạn đếm đến con số 12.
Do đó, bằng phương pháp này, với hai bàn tay bạn sẽ đếm được 24 số. Khi sử dụng cách đếm này, cũng không có thứ tự ưu tiên cho ngón tay đặc biệt nào cả.
Chỉ cần dùng ngón cái làm công cụ đếm, bạn có thể đếm các ngón theo thứ tự từ gần ra xa, từ xa lại gần tùy thích, miễn là, giống quy tắc phía trên: một đốt ngón tay không được đếm hai lần.
Tận dụng các đốt ngón tay sẽ giúp chúng ta đếm được nhiều hơn.
Trình độ chuyên nghiệp: 576
Ở một số nơi, người ta dùng một tay để đếm tay còn lại. Cụ thể hơn, với phương pháp này, bạn dùng một tay làm các mốc đếm để đếm các đốt tay của tay còn lại.
Ví dụ, bạn dùng tay trái làm "bộ đếm mốc", còn tay phải làm "bộ đếm lặp". Để bắt đầu, bạn đếm các đốt ngón tay của bàn tay phải, và khi đếm đến hết só 12, bạn chạm ngón tay trái vào đốt ngón tay đầu tiên trên bàn tay trái của mình.
Sau đó, bạn tiếp tục đếm từ 1 đến 12, rồi chạm vào đốt ngón tay tiếp theo của bàn tay trái. Cứ như vậy, với 12 đốt ngón tay ở tay phải và 12 đốt ngón tay ở tay trái, bạn có thể tự tin đếm đến 12*12=144 rồi nhé.
Cách thức này sẽ còn giúp chúng ta đếm được nhiều hơn nếu chúng ta coi các đường phân tách các đốt ngón tay cũng là một đơn vị đếm. Mỗi ngón tay có ba đốt, tương ứng với ba vạch phân tách đốt ngón tay.
Nói một cách khác, mỗi ngón tay chúng ta có thể đếm được 6 số, và một bàn tay cho phép chúng ta đếm được 6*4=24 số. Do đó, với cách thức trên, bạn có thể đếm được 576 số.
Trình độ chuyên gia: 1023
Giờ chúng ta sẽ tiến tới một số trình độ toán học phức tạp hơn trong nghệ thuật đếm bằng ngón tay. Những nhà toán học thông minh nhất, khi thể hiện tài năng về tính toán, đều sử dụng kỹ thuật "ký hiệu vị trí".
Cách thức này xuất phát từ kiến thức toán học về hệ thập phân: mỗi một số trong hệ thập phân đều có một cách nhất định để biểu thị cho chính nó. Nói cách khác, tất cả các con số chúng ta sử dụng hàng ngày đều được biểu thị bằng tập hợp các phép toán liên quan đến lũy thừa của 10.
Ví dụ: Số 257 được biểu thị bằng phép toán: 2*102 + 5*101 + 7*100
Sức mạnh của hệ nhị phân đánh dấu tầm quan trọng của những ngón tay
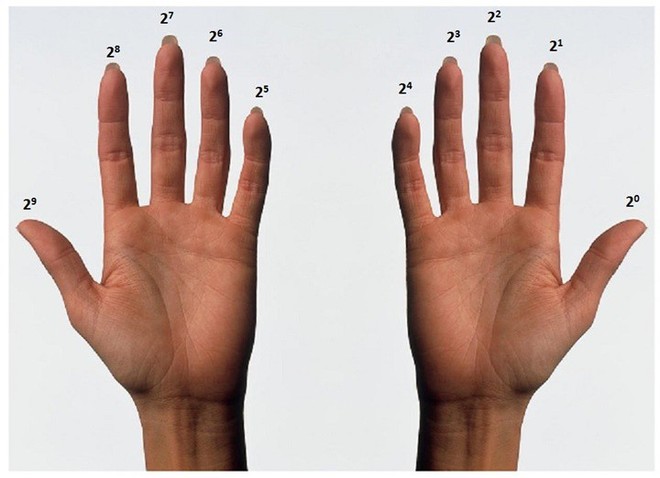
Cũng giống như vậy, nếu chúng ta sử dụng hệ nhị phân đối với những ngón tay để đếm, thì số 86 sẽ được biểu thị là 1010110, được diễn giải khi biến đổi sang hệ thập phân như sau: 1*26 + 0*25 + 1*24 + 0*23 + 1*22 + 1*21 + 0*20
Vì ngón tay của chúng ta chỉ có hai vị trí cơ bản: gập và duỗi, do đó, việc đếm theo hệ thập phân là rất khó, nếu không muốn nói là không thể. Bởi vậy, chúng ta có thể sử dụng hệ nhị phân dựa trên các lũy thừa của 2 để gán giá trị cho từng ngón tay một: ngón tay duỗi được đếm là 1, và ngón tay gập đếm là 0.
Cách thức này giúp bạn biểu thị con số là tổng số các lũy thừa của 2 (từ lũy thừa 0 lên đến lũy thừa 9 – tương ứng với 10 ngón tay) nhân với con số biểu thị của từng ngón tay (0 hoặc 1). Và nếu tất cả các ngón tay đều duỗi, thì số cao nhất chúng ta có thể đếm là 1+2+4+8+16+32+64+128+256+512=1023
Máy tính sử dụng hệ nhị phân để chuyển hóa và hiểu các con số của hệ thập phân, bởi chúng chỉ có thể hiểu hai tín hiệu số là CAO và THẤP. CAO được hiểu là 1, và THẤP được hiểu là 0.
Điều này chứng minh rằng, bằng mọi cách tính toán, dù phức tạp đến đâu, đều có thể được thực hiện bằng hệ nhị phân. Dĩ nhiên, 10 ngón tay của chúng ta không có sức mạnh tuyệt vời đến vậy, mà chỉ dừng lại ở con số 1023 như đã nói phía trên.

Máy tính chỉ sử dụng và hiểu hai tín hiệu CAO và THẤP
Ngoài những lợi ích của việc ứng dụng kỹ thuật tính toán dựa trên ký hiệu vị trí trên, chúng tôi cũng cần đưa ra những hạn chế của nó. Nếu bạn muốn nói bạn cần 4 quả chuối, thì việc bạn đưa 4 ngón tay biểu thị số chuối bạn cần trông sẽ dễ hiểu và tạo ấn tượng ghi vào não của người đối diện nhanh hơn.
Nếu bạn biểu thị số 22 bằng cách giơ ngón tay giữa lên thì có vẻ không hợp lý lắm, vì người đối diện sẽ hiểu ra một hàm ý khác. Và trong một số trường hợp, có thể bạn sẽ gặp rắc rối vì cách biểu thị con số này của mình.
Tuy nhiên, cách thức này khá tiềm năng khi sử dụng để tính các phép toán cơ bản với đối tượng học sinh lớn tuổi hơn một chút.
Đếm trên hệ nhị phân bằng cách sử dụng các ngón tay cho thấy bạn có thể đếm tổng số nhiều hơn con số 10 và thực hiện phép nhân nhanh chóng bằng con số 2 cùng các lũy thừa của 2.
Trình độ bác học: dương vô cực
Nếu một người khéo léo đủ để có thể uốn cong ngón tay theo 3 đốt (không chỉ dừng lại ở hai vị trí gập và duỗi), thì họ sẽ nâng khả năng đếm của mình vượt trên cả con số 1053. Bởi với cách duỗi ngón tay khéo như vậy, cơ sở đếm không còn là 2, mà là 3. Do đó, con số họ có thể đếm lên tới 59058 (=310-1). Thật tuyệt vời.
Giờ chúng ta đã thấy rằng, bàn tay con người rất hữu ích trong việc đếm số. Nếu ngón tay của chúng ta tạo được càng nhiều hình dáng, chúng ta càng đếm được nhiều số.
Các cách thức chúng tôi đưa ra phía trên đều dựa trên thực tế rằng chúng ta luôn cần các tín hiệu trực quan về các con số được biểu thị bằng hình dáng và số lượng các ngón tay của chúng ta đưa ra. Dĩ nhiên, nếu chúng ta bỏ qua cách thức đếm ngón tay mà chỉ đếm dựa trên những cái chạm, thì chúng ta có thể đếm xa đến vô cùng.
Ví dụ, nếu chúng ta sử dụng ngón tay cái chạm nhẹ vào các ngón tay khác để đếm, hết một lượt các ngón tay, lại quay lại từ ngón tay đầu tiên và tiếp tục đếm, thì chúng ta sẽ đếm đến bao nhiêu cũng được.
Về lý thuyết, với cách thức này, khi đếm lên con số càng cao, chúng ta càng dễ nhầm lẫn. Tuy nhiên, trên thực tế, con người chúng ta đếm theo cách này rất tuyệt vời và chuyên nghiệp!

