Hãng tin BBC của Anh đã tiến hành cuộc khảo sát lấy ý kiến bình chọn của độc giả về các phương trình toán học có ý nghĩa nhất.
Sau đây là 3 phương trình được độc giả bình chọn nhiều nhất. 3 phương trình này là tiền đề phát triển của các ngành vật lý, hóa học, khám phá vũ trụ…
Phương trình Dirac

Phương trình này của nhà vật lý người Anh Paul Dirac (1902 – 1984), người sống cùng thời với nhà bác học Albert Einstein. Năm 1933, ông từng cùng nhận giải Nobel vật lý cùng với Erwin Schrodinger cho giả thuyết lượng tử.
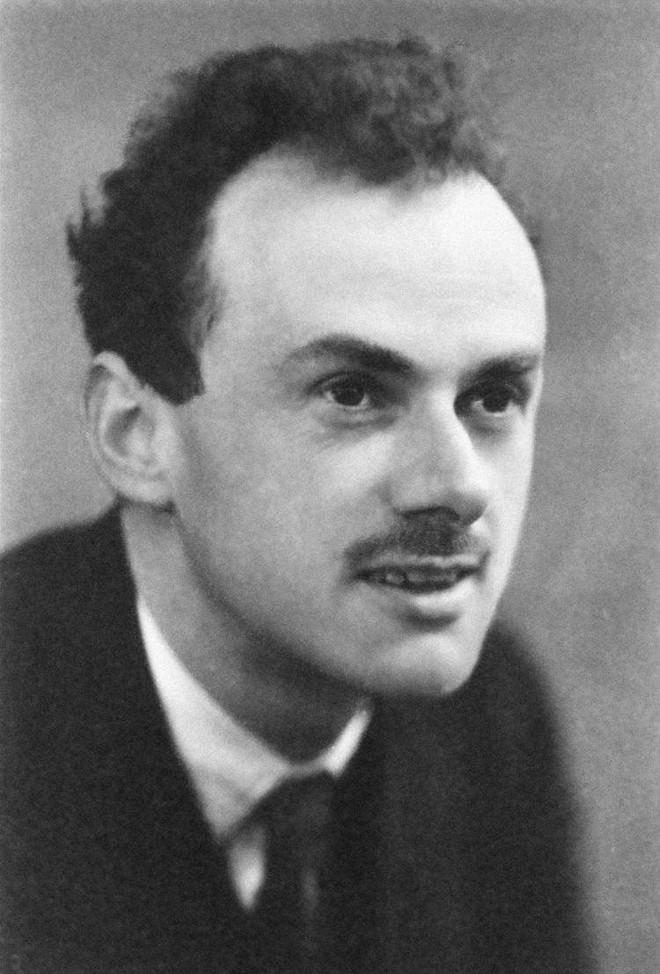
Nhà vật lý Paul Dirac.
Phương trình của Paul Dirac kết hợp với thuyết tương đối của Albert Einstein dùng để tính chuyển động của các vật thể với tốc độ ánh sáng, với cơ học lượng tử được mô tả là hoạt động của những phân tử rất nhỏ.
Bằng cách tìm phương trình giải thích các electron xoay thế nào khi đạt tốc độ ánh sáng, Paul Dirac đã bước đầu đưa ra giả thuyết lượng tử và dự đoán sự tồn tại của kháng thể, mà lúc đó các nhà vật lý chưa hề nghĩ tới hay quan sát được.
Phương trình Dirac miêu tả cấu trúc tinh tế trong dải phổ hydro theo cách rất phức tạp. Phương trình cũng là sự hiệu chỉnh lý thuyết bằng việc đưa ra các hàm sóng chứa một số thành phần trong lý thuyết của Pauli về chuyển động xoay.
Hàm sóng trong lý thuyết của Dirac là các vectơ với bốn thành phần là các số phức (còn gọi là bispinor).
Hai trong số chúng giống với hàm sóng Pauli trong giới hạn phi tương đối tính, khác với phương trình Schrödinger mà miêu tả hàm sóng chỉ có một thành phần phức. Hơn nữa, trong trường hợp khối lượng gán bằng 0, phương trình Dirac trở thành phương trình Weyl.
Mặc dù ban đầu Dirac không hoàn toàn đánh giá được đầy đủ ý nghĩa quan trọng của phương trình này.
Nhưng với hệ quả của việc giải thích chuyển động xoay trong sự thống nhất giữa cơ học lượng tử với thuyết tương đối hẹp, phương trình Dirac là một trong những thành tựu to lớn của vật lý lý thuyết.
Phương trình Dirac là sự hội tụ trí tuệ của nhà bác học Newton, Maxwell và Einstein. Trong lý thuyết trường lượng tử, phương trình Dirac được giải thích theo nghĩa khác nhằm miêu tả trường lượng tử tương ứng với các hạt có chuyển động xoay.
Đồng nhất thức Leonhard Euler
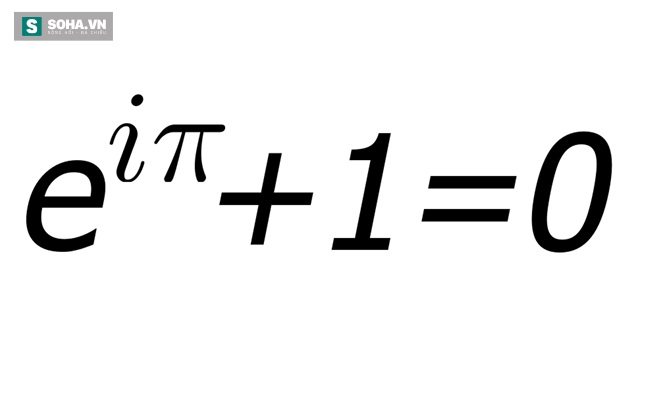
Nhà toán học Leonhard Euler (1707 - 1783), người Thụy Sĩ, được mệnh danh là “Mozart trong toán học” bởi ông có sức làm việc phi thường nhất.

Chân dung nhà toán học Leonhard Euler.
Các công trình khoa học của ông thuộc về nhiều ngành lĩnh vực khác nhau để lại cho hậu thế nhiều vô kể.
Tính ngang bằng của đồng nhất thức này của Leonhard Euler trông có vẻ đơn giản hơn phương trình của Diract.
Nhưng đồng nhất thức nhìn tưởng như đơn giản này lại thâu tóm một số nguyên tắc toán học cơ bản nhất.
Phương trình chứa 5 con số quan trọng nhất trong toán học là 1, 0, Pi, i, và e với 3 phép tính cơ bản trong toán học là: cộng, nhân và mũ hóa.
Chữ “I” ở đây là con số tưởng tượng, bình phương gốc của -1. Chữ “e” là con số tương đương 2.71828, nhưng giống như Pi, e vô tỉ.
Nhìn tưởng như đơn giản nhưng đồng nhất thức này có vai trò rất quan trọng trong mọi khía cạnh cơ bản của toán học.
Con số Pi
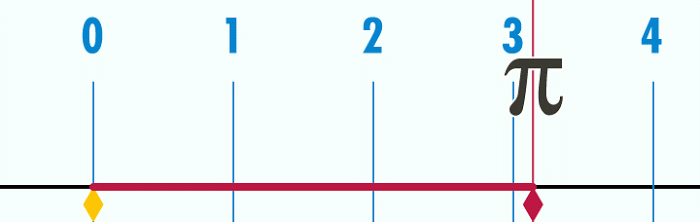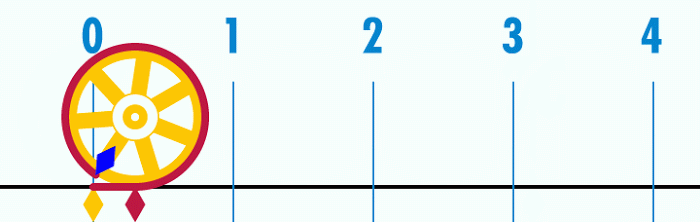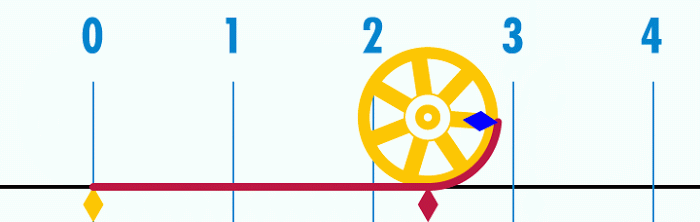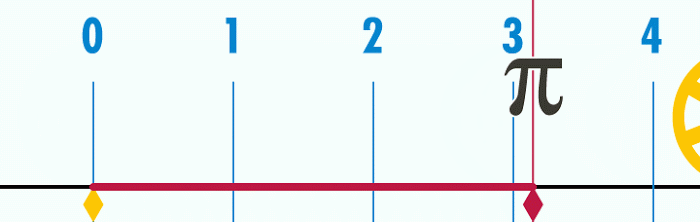
Biểu diễn số Pi.
Con số Pi có lẽ được sử dụng nhiều nhất trong trường phổ thông. Pi là tỷ số của chu vi của một đường tròn với đường kính của đường tròn đó
Pi tương đương 3.14159, nhưng nó cũng vô tỉ. Người Babylon cổ đại nghĩ ra con số Pi cách đây 4.000 năm và vẫn được sử dụng đến ngày nay.
Số Pi giúp chúng ta khám phá các hành tinh, phóng tàu vũ trụ, thậm chí còn được ứng dụng vào tính đường xoắn ốc ADN kép.
Tính siêu việt của Pi kéo theo sự vô nghiệm của bài toán cầu phương. Các con số thập phân của Pi dường như xuất hiện theo một thứ tự ngẫu nhiên, mặc dù người ta chưa tìm được bằng chứng cho tính ngẫu nhiên này.
Hàng ngàn năm qua, các nhà toán học đã nỗ lực mở rộng hiểu biết của con người về số Pi bằng việc tính ra giá trị của nó với độ chính xác ngày càng cao hơn.
*Nguồn: Tech Insider


