Vào năm 2019, một tài khoản Twitter tên @pjmdoll đã đặt ra một câu hỏi toán học tưởng chừng vô cùng đơn giản: 8:2(2 + 2) = ? Bài toán thuộc cấp độ tiểu học sau đó đã thu hút tới 13 triệu lượt thích và hàng trăm ngàn bình luận chỉ sau một tháng. Và đến hiện tại, mỗi khi bài toán được đưa ra lại, kết quả vẫn khiến nhiều người ngỡ ngàng.
Phép toán này đã làm thế giới điên đầu và chia rẽ mãi một hồi.
Vậy điều gì khiến phép tính căn bản này trở thành đề tài tranh cãi? Lý do là vì mọi người lại đưa ra 2 kết quả hoàn toàn khác nhau và đều không hiểu vì sao lại có đáp án khác nữa. Cụ thể, có 2 luồng ý kiến đáp án là 1 hoặc 16. Người tính ra 1 kêu gọi những người theo phe 16 phổ cập lại kiến thức đáng quan ngại của mình. Người tính ra 16 lại khẳng định phe 1 nên xin lỗi giáo viên cấp 1.

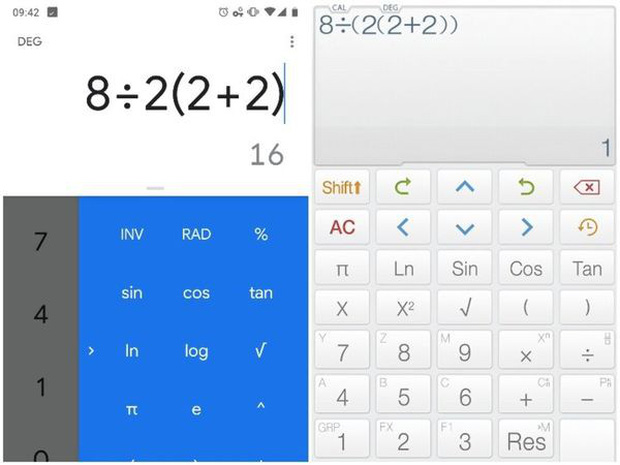
Thậm chí bấm máy tính cũng có thể ra 2 kết quả khác nhau.
Theo một cuộc bình chọn trực tuyến, người ra đáp án 1 chiếm đa số hơn. Theo nguyên tắc toán học, hiển nhiên phép tính trong ngoặc sẽ được tính trước vì vậy sẽ thành 8 : 2 x 4 = ?. Sau đó, mọi người lấy 2 x 4 và có phương trình: 8 : 8 = 1.
Thế nhưng, sự thật là đáp án của phép toán này phải là 16. Rất nhiều người đều đã mắc chung một cái bẫy đơn giản đến không ngờ. Sau khi cộng xong phép tính ưu tiên trong ngoặc, chúng ta phải áp dụng luật nhân chia trước, cộng trừ sau và tính từ trái sang phải. Vì thế phép chia phải được làm trước phép nhân, thế nhưng mọi người đều "tiện thể" nhân luôn nên đã bị đảo lộn.
Sau khi phá ngoặc chúng ta phải làm phép chia trước mới đúng.
Trên thực tế, phép tính này sẽ được viết đủ là 8 : 2 x (2 + 2). Theo thứ tự ưu tiên trong ngoặc, ta sẽ có phép toán 8 : 2 x (4). Tiếp tục dùng tới thứ tự từ trái qua phải, ta sẽ lấy 8:2 trước rồi đêm kết quả nhân với 4 để ra đáp án là 16.
Nếu muốn đáp án ra là 1, bài toán cần phải được viết như sau: 8 : (2(2 + 2)).
Theo nhà toán học người Mỹ Presh Talwalkar đến từ Đại học Stanford, việc có quá nhiều người tính ra là 1 cũng không phải là lạ. Đây vẫn được coi là đáp án đúng nếu chúng ta sống ở thời điểm... 100 năm trước.
Lý do là vì trước đây, thứ tự ưu tiên trong toán học được áp dụng theo quy ước tên BODMAS. Theo BODMAS thì việc nhân 2 luôn với kết quả trong ngoặc là chính xác. Tuy nhiên ngày nay thế giới đã áp dụng quy ước mới là PEMDAS không còn chấp nhận thứ tự này nữa.
Nguồn: Insider



